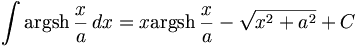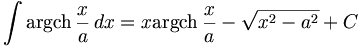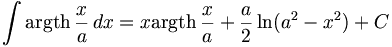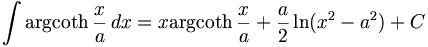Vendredi 19 Décembre 2025
Rechercher 🔍
Mathématiques

Primitives de fonctions hyperboliques réciproques - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.
Cet article fait partie de la série
Primitives de fonctions
Rationnelles
Logarithmes
Exponentielles
Irrationnelles
Trigonométriques
Hyperboliques
Circulaires réciproques
Hyperboliques réciproques

Cet article donne les primitives des fonctions réciproques des fonctions hyperboliques.

On suppose a≠0.

\int \operatorname{argsh}\,\frac{x}{a}\,dx=x \operatorname{argsh}\,\frac{x}{a}-\sqrt{x^2+a^2}+C
\int \operatorname{argch}\,\frac{x}{a}\,dx=x \operatorname{argch}\,\frac{x}{a}-\sqrt{x^2-a^2}+C
\int \operatorname{argth}\,\frac{x}{a}\,dx=x \operatorname{argth}\,\frac{x}{a}+\frac{a}{2}\ln(a^2-x^2)+C
\int \operatorname{argcoth}\,\frac{x}{a}\,dx=x \operatorname{argcoth}\,\frac{x}{a}+\frac{a}{2}\ln(x^2-a^2)+C
miniature
💥 Cette tour Eiffel gravée en 3D dans du silicium montre l'avenir des semi-conducteurs
miniature
🌀 Une étoile dévoile l'entrainement de l'espace-temps près d'un trou noir
miniature
⁉️ La momie égyptienne "Intouchable" qu'aucun scientifique n'ose ouvrir
miniature
☄️ L'objet interstellaire 3I/ATLAS s'approche au plus près de la Terre ce vendredi
miniature
🔭 Une planète 'Tatooine' découverte à une distance jamais vue de ses étoiles jumelles
miniature
💔 En amour, sachez ce que vous voulez ! Selon une étude, le flou amoureux nuirait à votre bien-être
miniature
🦖 Découverte exceptionnelle de plus de 16 000 empreintes de dinosaures en Bolivie
miniature
🌡️ La chaleur cause un retard intellectuel chez les enfants
miniature
1
🌟 Ces photographies d'étoiles de matière noire qui intriguent les scientifiques
miniature
🍬 Cet édulcorant populaire au sucre est transformé finalement par l'organisme en... sucre
miniature
💥 Pourquoi l'Univers ne s'est-il pas auto-annihilé à sa naissance ?
miniature
🙊 Notre cerveau reconnaît la voix de nos cousins primates
miniature
🪐 Vie extraterrestre sur TRAPPIST-1 e: son atmosphère étudié de très près
miniature
🌊 De millénaires à quelques heures: ils accélèrent un processus de captation de carbone
miniature
⚫ Comment les trous noirs pourraient révéler l'invisible matière noire
miniature
🌍 La taille du trou dans la couche d'ozone en 2025 surprend et rassure
miniature
⚡ Une nouvelle explication pour les radiations extrêmes d'Uranus
miniature
🌋 Une éruption volcanique pourrait-elle être à l'origine de la peste noire en Europe ?
miniature
⚛️ Informatique quantique: un développement similaire à l'informatique des années 1970 ?
miniature
👀 Pourquoi les yeux grandissent encore à l'âge adulte ?
miniature
🔭 Une surprenante jumelle de la Voie Lactée découverte dans l'Univers bébé
miniature
🦠 Les mirusvirus, ces virus géants qui continuent à nous surprendre
miniature
🚪 Pyramides de Gizeh: découverte d'une potentielle entrée cachée
miniature
⚫ Voici la plus fidèle simulation d'un trou noir à ce jour
miniature
☕ Une étude révèle que, à cette consommation précise, le café ralentirait le vieillissement
miniature
⚛️ Les formules d'un génie du passé ressurgissent dans la physique des trous noirs
miniature
🌊 Un tsunami médiéval exceptionnel dans les Caraïbes
miniature
🖋️ Les systèmes de sécurité les plus robustes des IA se laissent berner par de simples poèmes
miniature
🌟 Une naine brune et une exoplanète géante observées directement avec une précision inédite
miniature
🧠 Consommation de cannabis pendant la grossesse et retard du développement cognitif
miniature
🔄 Ce filtre, inspiré des sardines, capte 99% des microplastiques d'un lave-linge
miniature
✨ Notre galaxie possède une signature chimique typique, l'explication trouvée
miniature
☠️ Quand la bactérie responsable de la tuberculose fabrique son propre poison
miniature
🪐 Des astronomes découvrent une longue chaîne de galaxies en rotation synchronisée
miniature
🧠 Une simple molécule contrôle vos habitudes et vos envies irrésistibles
miniature
🧠 Cet implant cérébral ultra-mince permet de connecter efficacement son cerveau à une IA
miniature
🦠 Evolution: nos défenses immunitaires semblables à celles des... bactéries
miniature
🛰️ Une IA trouve une faille à la NASA permettant de prendre le contrôle des missions spatiales
miniature
🌋 Un système hydrothermal majeur découvert en Méditerranée
miniature
🪐 Un espoir de vie extraterrestre sur TRAPPIST-1e, malgré les fureurs de son étoile
miniature
🌱 Remplacer les engrais par des "déchets"
miniature
💥 Des physiciens éliminent une théorie majeure sur les neutrinos
miniature
💉 En test, un vaccin universel contre le cancer montre une efficacité exceptionnelle
miniature
🕰️ Le temps sur Mars avance plus vite que sur Terre, et ce n'est pas négligeable
miniature
🌍 Les tremblements de terre, un boost inattendu pour la vie invisible
miniature
✨ Deux étoiles massives nous ont frôlé, laissant des traces encore visibles
miniature
🧠 Cerveau: une autre source d'énergie que le sucre pour les neurones
miniature
🧬 La vie complexe est apparue près d'un milliard d'années plus tôt qu'estimé
miniature
🌡️ Comment la température influence la conscience de notre propre corps
miniature
1
🔭 Un signal gravitationnel pourrait révéler des trous noirs primordiaux
Page générée en 0.098 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise