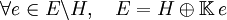Hyperplan - Définition
En algèbre linéaire, les hyperplans sont définis dans la théorie des espaces vectoriels.
Définition
Soit E un

On dit que H est un hyperplan de E si H est de codimension 1.
Remarques :
- Dans un espace de dimension finie n, les hyperplans sont donc les sous-espaces vectoriel de dimension n-1.
- Dans
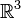
Caractérisation
On montre l'équivalence des propriétés suivantes :
- H est un hyperplan
- Il existe une droite D telle que
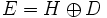
-