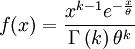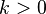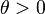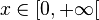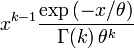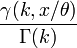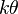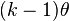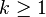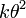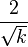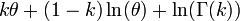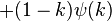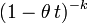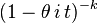Distribution Gamma - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

**Loi Gamma**
Densité de probabilité / Fonction de masse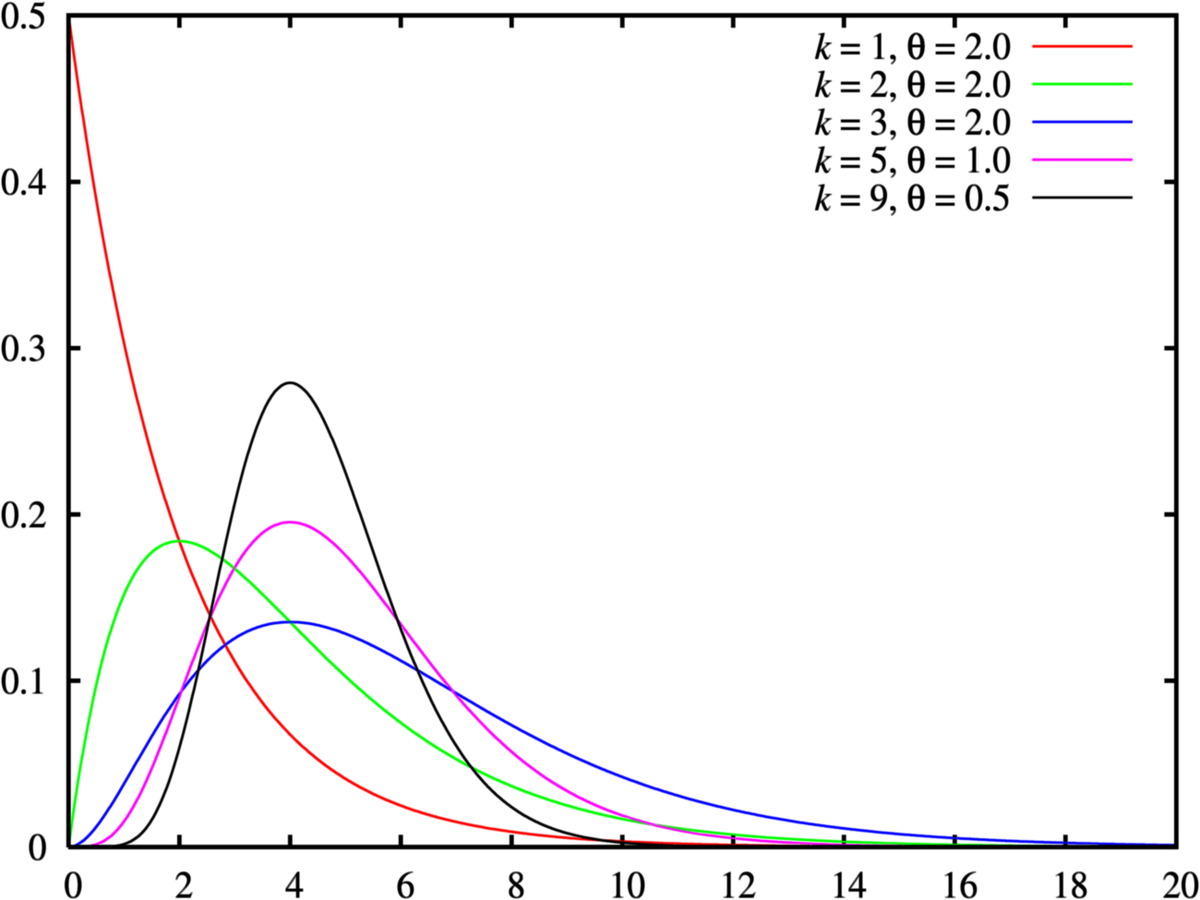
Fonction de répartition >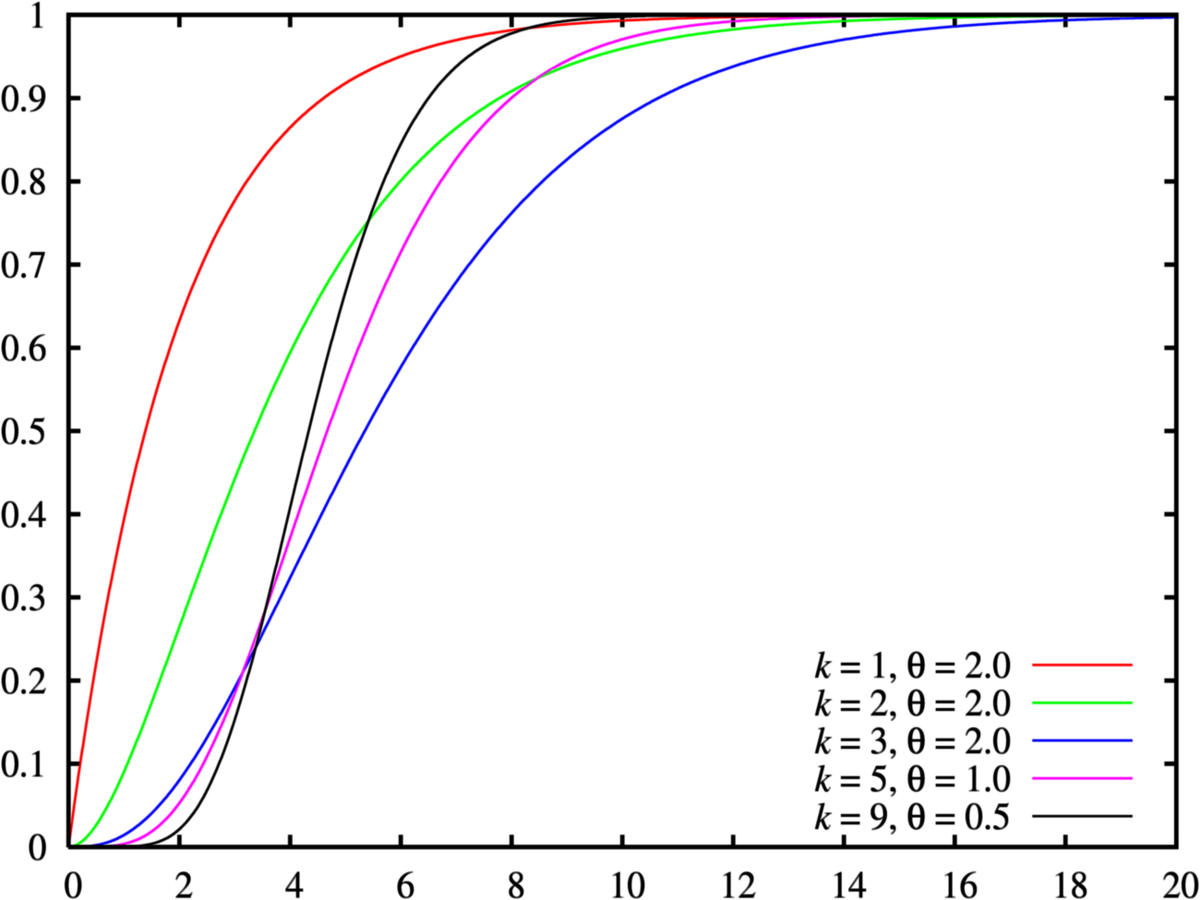
Paramètres	$k width=$ 0\," > réel $\theta width=$ 0\," > réel
Support	$x \in [0,+ \infty[$
Densité de probabilité (fonction de masse)	$x^{k-1} \frac{\exp\left(-x/\theta\right)}{\Gamma(k)\,\theta^k}$
Fonction de répartition	$\frac{\gamma(k, x/\theta)}{\Gamma(k)}$
Espérance	$k \theta\,$
Médiane (centre)
Mode	$(k-1) \theta\,$ for $k \geq 1\,$
Variance	$k \theta^2\,$
Asymétrie (skewness)	$\frac{2}{\sqrt{k}}$
Kurtosis (non-normalisé)	$\frac{6}{k}$
Entropie	$k\theta+(1-k)\ln(\theta)+\ln(\Gamma(k))\,$ $+(1-k)\psi(k)\,$
Fonction génératrice des moments	$(1 - \theta\,t)^{-k}$ pour $t < 1 / θ$
Fonction caractéristique	$(1 - \theta\,i\,t)^{-k}$

Une variable aléatoire X suit une loi Gamma si sa fonction de densité de probabilité peut se mettre sous la forme :

$f(x) = \frac{{x^{k - 1} e^{ - \frac{x}{\theta }} }}{{\Gamma \left( k \right) \theta ^k }}$ où $k$ et $θ$ sont les paramètres (strictement positifs) de la loi.

🌍 Découverte: cette règle universelle régit toute vie sur terre

⏳ L'Univers pourrait disparaître plus tôt que prévu: ce que révèle cette étude

🌍 Les dernières mesures révèlent un niveau de CO₂ jamais vu depuis 4 millions d'années

🛡️ Le paradoxe des gangs de rue

💰 Quelle quantité d'or existe-t-il vraiment sur Terre ?

🦟 Pourquoi les moustiques sont plus nombreux et piquent davantage en été ?

⚫ Ces trous noirs interagissent avec la lumière fossile du Big Bang

🦕 Et si les dinosaures détenaient le secret pour vaincre le cancer ?

😎 Comment font les lunettes de soleil pour filtrer les UV ?

🚶‍♂️‍➡️ La marche des babouins éclaire l'évolution de la bipédie humaine

🔭 James Webb capture cette image directe d'une étrange planète à 60 années-lumière

🦋 Pourquoi et comment les chenilles deviennent-elles des papillons ?

🔭 Voici la plus grande carte de l'Univers. Ses révélations sont surprenantes !

😴 Penser que l'on est éveillé alors que l'on dort, normal ?

🌊 Ce cratère raconte l'histoire de l'eau sur Mars

🐝 Comment les fleurs attirent-elles les insectes pollinisateurs ?

💥 La collision entre notre Voie lactée et la galaxie d'Andromède remise en question

🎶 Pourquoi les oiseaux chantent-ils autant et si fort au printemps ?

💡 Générer de la lumière à partir du vide, c'est possible

Découverte d'un deuxième système d'apprentissage dans le cerveau

☀️ Comment se produit un coup de chaleur et comment s'en protéger ?

⚽ Comment fonctionne la physique d'un tir puissant au foot ?

🧠 Un algorithme révèle comment notre cerveau se motive

🔭 Une si grande planète orbite une si petite étoile, comment est-ce possible ?

🐋 Les baleines développent de nouvelles méthodes pour communiquer avec nous

🥚 Le noyau de Mars sent l'œuf pourri

🧠 On sait enfin pourquoi le sémaglutide fait maigrir

🌱 La vie pourrait renaître sur Europe après la mort de la Terre

🌿 Confirmation scientifique: ce remède ancestral fait naturellement maigrir, et pas qu'un peu !

💥 Des astronomes identifient les plus puissantes explosions depuis le Big Bang

🦕 Ce crâne de stégosaure, le plus complet jamais découvert, réécrit l'histoire

🛏️ Les punaises de lit, ces compagnons indésirables depuis la préhistoire

🕸️ Connaissez-vous la toile cosmique, l'architecte de l'Univers ?

🌋 L'éruption de l'Etna vue depuis l'espace

🐋 Il y a 20 000 ans, l'Homme fabriquait des outils avec des os de baleines

🟠 Quel est le rôle de ce labyrinthe sur Mars ?

🎯 Cette stratégie innovante contre le cancer du sein offre une survie de 100%

💥 Le pulsar à trou noir: un objet qui intrigue les astrophysiciens

🐒 Première: ces singes kidnappent les bébés d'une autre espèce

🌍 Découverte d'une super-Terre à l'habitabilité intermittente

🧠 Ces cellules pourraient jouer un rôle bien plus important que les neurones dans la mémoire

🛰️ Une carte photographique de la Terre toutes les 35 minutes

Pourquoi l'oxygène est-il si indispensable à autant d'êtres vivants ?

🐱 Pourquoi certains chats miaulent et ronronnent plus que d'autres ?

Découverte: un antidouleur sans effets secondaires

🤔 Ces expériences remettent en question un concept fondamental de la thermodynamique

Le cannabis réduit de moitié la fonction des vaisseaux sanguins

Les différences hommes-femmes ne sont pas que génétiques

🦴 Des paresseux géants de plusieurs tonnes parcouraient autrefois l'Amérique

James Webb découvre une nouvelle population de trous noirs supermassifs

Page générée en 0.099 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise