Médiane - Définition
Utilisation du terme
- Revue Médiane
- Europe médiane
- Filtre médian
- Francie médiane
- Voie médiane
- Point médian
- Nerf médian
Mathématiques
Le terme de médiane, du latin medius, qui est au milieu, possède plusieurs acceptations en mathématiques :
Géométrie plane
- En géométrie, les médianes d'un triangle sont les segments de droites joignant les sommets aux milieux des côtés opposés.
- La médiane issue du sommet A d'un triangle ABC est le segment [AM] où M désigne le milieu du segment [BC]. Par extension mais aussi de manière plus rigoureuse, le nom de médiane s'applique à la droite (AM).
- Les trois médianes d'un triangle sont concourantes. Leur point d'intersection est le centre de gravité. Il est situé aux

- Le centre de gravité G vérifie la relation vectorielle :

-
- Dans un triangle une médiane sépare le triangle en deux triangles d'aires égales.
- Dans un triangle isocèle la médiane relative à la base est axe de symétrie du triangle et les deux autres médianes sont de longueur égale.
- Réciproquement si dans un triangle deux médianes sont de même longueur, le triangle est isocèle.
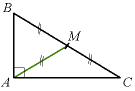
- Le dessin ci-contre montre que la médiane issue du sommet de l'angle droit dans un triangle rectangle mesure la moitié de l'hypoténuse.
- Réciproquement si dans un triangle la longueur d'une médiane est égale à la moitié de la longueur du côté correspondant, le triangle est rectangle.
- Théorème de la médiane
- Forme vectorielle du " théorème de la médiane " dans le triangle ABC où M est le milieu de [BC] :
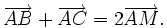
- Forme vectorielle du " théorème de la médiane " dans le triangle ABC où M est le milieu de [BC] :
-
- Le " deuxième théorème de la médiane " affirme que
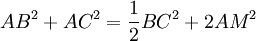
- Le " deuxième théorème de la médiane " affirme que
- Voir aussi l'article Triangle
- En géométrie toujours, les médianes du quadrilatère sont les segments reliant les milieux des côtés opposés.
Les médianes sont les diagonales du parallélogramme de Varignon, elles se coupent en leurs milieux.
-
- L'associativité des barycentres peut aussi justifier que le milieu des médianes est le centre de gravité du quadrilatère
(voir : barycentre).
- L'associativité des barycentres peut aussi justifier que le milieu des médianes est le centre de gravité du quadrilatère
Géométrie, dans l'espace
- En géométrie, dans l'espace cette fois-ci, on appelle médianes d'un tétraèdre les segments ayant pour extrémités un sommet du tétraèdre et le centre de gravité de la face opposée à ce sommet. Il y a donc 4 médianes dans un tétraèdre, elles se coupent en un point qui est l'isobarycentre du tétraèdre.
- Dans un tétraèdre régulier (toutes les faces sont des triangles équilatéraux), les médianes sont aussi les hauteurs (on dira que ce tétraèdre est orthencentrique... car, contrairement aux triangles, les hauteurs d'un tétraèdre ne sont pas forcément concourantes !). La molécule de méthane CH4 illustre ce cas : les sommets sont occupés par des atomes d'hydrogène ; l'atome de carbone se situe au point de rencontre des médianes !
Statistiques
- En Statistique, la médiane est la valeur qui permet de partager une série numérique en deux parties de même nombre d'éléments.
- C'est l'une des caractéristiques d'une série numérique, qu'il convient de bien distinguer de la moyenne même si ces deux valeurs sont voisines dans le cas d'une distribution équilibrée (voir l'article Critères de position). La médiane entre 2 points est son milieu. Le salaire médian désigne ainsi le palier divisant la société en deux parties égales: 50% de la population gagne moins que le salaire médian et l'autre moitié de la population gagne plus.
Voir Médiane (mathématiques élémentaires)

















































