Fonction génératrice - Définition
La liste des auteurs de cet article est disponible ici.
En mathématiques
En mathématiques, la fonction génératrice de la suite (an) est la série formelle définie par
On confond parfois la fonction génératrice et une fonction de la variable x. Cependant, il est utile de préciser qu'une fonction génératrice est avant tout une série formelle et que la fonction de la variable x correspondante risque de ne pas converger pour tout x.
- fonction génératrice de la suite constante 1 :
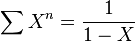
- fonction génératrice de la suite (n) :
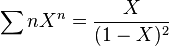
- fonction génératrice de la suite (n2) :
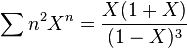
- fonction génératrice de la suite
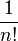
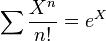
On parle aussi de fonction génératrice exponentielle de la suite (an) définie par la série formelle
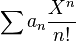
Lorsque l'on travaille plutôt avec l'inverse de X, la variable z=1/X, on parle alors de la transformée en Z,
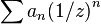
On peut retrouver la suite initiale (an) à partir de la fonction génératrice F(X) (resp. la fonction génératrice exponentielle E(X)) selon les formules
En probabilité
Définition
Soit X une variable aléatoire entière et positive, la fonction génératrice de X est la série entière:

où
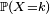
Fonctions génératrices de lois usuelles
- Pour la loi de Poisson de paramètre λ, on a

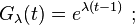
- Pour la loi binomiale de paramètres (n, p), on a
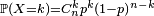
Propriétés
- Le rayon de convergence de cette série entière est toujours supérieur ou égal à 1.
- On peut remarquer que
![G_X(t)=\mathbb{E}[t^{ X}].](https://static.techno-science.net/illustration/Definitions/autres/1/14aeaa311e40a90772229b7abcfcad58_b6702ef55622363b8681dc1c62e62f8c.png)
- Si X admet une espérance
![\scriptstyle\ \mathbb{E}[X]\](https://static.techno-science.net/illustration/Definitions/autres/b/b007f12b3f096ca95412a411062e9a2f_8bd4d7b82606027ef254327c75b83501.png)
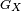
![\mathbb{E}[X]= \frac{dG_X}{dt} (t=1).](https://static.techno-science.net/illustration/Definitions/autres/a/ad7fd596c1438e12a8c391fabb60cbbd_af621df5ebb7af0e872cb40d4dca367b.png)
- Si X admet une variance
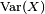
![\scriptstyle\ \mathbb{E}[X],\](https://static.techno-science.net/illustration/Definitions/autres/3/3a9d181dab4883ce91ab3bc9ff563dfa_607b1593fa2ed9cacbcaad0db33f6df6.png)
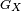
![Var[X]=\frac{d^2 G_X}{dt^2} (t=1) + \frac {dG_X} {dt} (t=1) - \left(\frac{dG_X}{dt} (t=1)\right)^2.](https://static.techno-science.net/illustration/Definitions/autres/2/2d2294013bf0d386450a2f3b85073e52_ff6bfe576e2ed7dc0ac0f9bb6451e64c.png)
- Si deux variables aléatoires réelles discrètes à valeurs dans
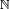
- Soient X et Y deux variables aléatoires réelles discrètes entières et positives. Si X et Y sont indépendantes alors on a:
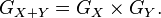
- Remarque : La réciproque est fausse.
- Si X1, X2, ..., Xn est une suite de variables aléatoires indépendantes, et si
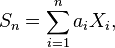
- où les ai sont des constantes, alors
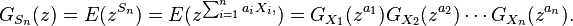
- Par exemple, si les Xi ont de plus même loi (et donc même fonction génératrice G ), alors
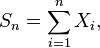
- a pour fonction génératrice :
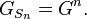
Composition des fonctions génératrices
La propriété suivante est particulièrement utile à l'étude des processus de Galton-Watson.
Théorème — Soit
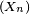
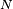
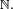
- On pose
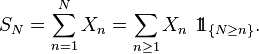
- On suppose que
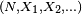
Alors :
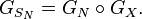
Généralisation aux variables aléatoires non entières
Cette notion de fonction génératrice se généralise aux variables aléatoires continues par les fonctions caractéristiques. Une autre notion utile est la fonction génératrice des moments.
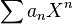
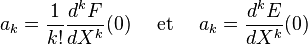
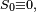
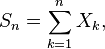
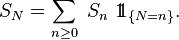
![\begin{align} G_{S_N}(z) &= \mathbb{E}\left[z^{S_N}\right]\\ &= \mathbb{E}\left[z^{\sum_{n\ge 0}\ S_n\ 1\!\!1_{\{N= n\}}}\right]\\ &= \mathbb{E}\left[\sum_{n\ge 0}\ z^{S_n}\ 1\!\!1_{\{N= n\}}\right]\\ &= \sum_{n\ge 0}\ \mathbb{E}\left[z^{S_n}\ 1\!\!1_{\{N= n\}}\right]\\ &= \sum_{n\ge 0}\ \mathbb{E}\left[z^{S_n}\right]\times\mathbb{E}\left[1\!\!1_{\{N= n\}}\right]\\ &= \sum_{n\ge 0}\ G_{S_n}(z)\times\mathbb{P}\left(N= n\right)\\ &= \sum_{n\ge 0}\ \mathbb{P}\left(N= n\right)\times \left(G_{X}(z)\right)^n\\ &= G_N\left(G_X(z)\right). \end{align}](https://static.techno-science.net/illustration/Definitions/autres/6/60757162c6922e00c25c1fe8d9773534_354d6c87ac1ab39ba2a5f3131adf56eb.png)

















































