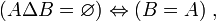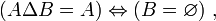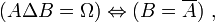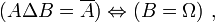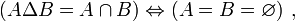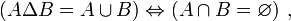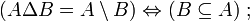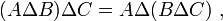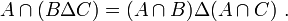Algèbre des parties d'un ensemble - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
Pour illustrer ces notions, soient A l'ensemble des hommes gauchers, et B l'ensemble des hommes blonds
Alors A ∩ B est l'ensemble de tous les gauchers blonds, alors que A ∪ B est l'ensemble de tous les hommes qui sont ou gauchers ou blonds, ou les deux. A \ B, en revanche, est l'ensemble de toutes les gauchers qui ne sont pas blonds, alors que B \ A est l'ensemble de tous les blonds qui ne sont pas gauchers. Enfin, A Δ B désigne l'ensemble de tous les hommes qui sont soit blonds, soit gauchers, mais pas les deux à la fois.
Maintenant supposons que C soit l'ensemble de tous les hommes âgés de plus de 1000 ans. Dans ce cas, A ∩ C est l'ensemble de tous les gauchers de plus de 1000 ans. Mais aucun homme n'a plus de 1000 ans (C est l'ensemble vide : Ø), donc A ∩ C doit être vide aussi.
Nous avons énuméré sans démonstration plusieurs propriétés simples des opérations sur les ensembles. Ces propriétés peuvent être visualisées avec les diagrammes de Venn.
Différence symétrique
Définition
Pour tout ensemble A et tout ensemble B, il existe un ensemble dont les éléments sont ceux qui appartiennent soit à A, soit à B, mais pas aux deux à la fois : la différence de A U B et de A ∩ B. On l'appelle la différence symétrique de A et de B et on le note « A Δ B » (lire « A delta B »). On peut l'écrire sous diverses formes :
Cette dernière expression justifie l'appellation de différence symétrique donnée à cette opération.
Propriétés
Pour tout ensemble Ω et tous sous-ensembles A, B, C de Ω, on a les propriétés suivantes :
- DS1 (commutativité) : la différence symétrique de deux ensembles ne dépend pas de l'ordre dans lequel ces ensembles sont pris :
- DS2 (Ø neutre) : la différence symétrique de l'ensemble vide et d'un autre ensemble redonne cet ensemble :
- DS3 (involutivité) : la différence symétrique de tout ensemble avec lui-même donne l'ensemble vide :
- DS4 (inversibilité) : A est inversible pour Δ (car son inverse est lui-même, d'après l'involutivité),
- DS5 (régularité, conséquence de l'inversibilité) : si les différences symétriques d'un ensemble avec deux autres ensembles sont égales entre elles, alors ces deux autres ensembles sont égaux entre eux :
- DS6 (Ω élément inverseur) : la différence symétrique d'un ensemble et du référentiel donne le complément absolu de cet ensemble :
- DS7 : la différence symétrique d'un ensemble et de son complément absolu redonne le référentiel :
- DS8 : le complément absolu de la différence symétrique de deux ensembles est égal à la différence symétrique de l'un des deux ensembles avec le complément absolu de l'autre ensemble :
- DS9 : A \ B et B \ A sont complémentaires l'un de l'autre dans A Δ B :
- DS10 : A Δ B et A ∩ B sont complémentaires l'un de l'autre dans A U B :
- DS11 : la différence symétrique de deux ensembles est vide si et seulement si les deux ensembles sont égaux :
- DS12 : la différence symétrique de deux ensembles est égale à l'un des deux ensembles si et seulement si l'autre ensemble est vide :
- DS13 : la différence symétrique de deux ensembles est égale au référentiel si et seulement si les deux ensembles sont complémentaires absolus :
- DS14 : la différence symétrique de deux ensembles est égale au complément absolu de l'un d'entre eux si et seulement si l'autre ensemble est le référentiel :
- DS15 : la différence symétrique de deux ensembles est égale à leur intersection si et seulement si les deux ensembles sont vides :
- DS16 : la différence symétrique de deux ensembles est égale à leur réunion si et seulement s’ils sont disjoints :
- DS17 : la différence symétrique de deux ensembles est égale à la différence de l'un avec l'autre si et seulement si l'un est inclus dans l'autre :
- DS18 (associativité) : la différence symétrique de trois ensembles ne dépend pas de l'ordre dans lequel les opérations sont effectuées :
- DS19 (distributivité de ∩ par rapport à Δ) : l'intersection d'un ensemble avec la différence symétrique de deux autres ensembles est égale à la différence symétrique des intersections du premier ensemble avec chacun des deux autres :
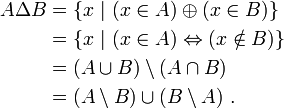
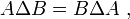
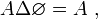
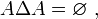
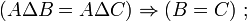
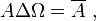
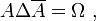
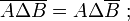
![[~A \Delta B=(A\setminus B)\cup(B\setminus A)~]\land[(A\setminus B)\cap(B\setminus A)=\varnothing~]~,](https://static.techno-science.net/illustration/Definitions/autres/c/c42eca1be60a790cd3b2b9bbccbe4e2b_febfbb64ba52514a2f82410e8fe49d8e.png)
![[~A\cup B=(A\Delta B)\cup(A\cap B)~]\land[~(A\Delta B)\cap(A\cap B)=\varnothing~]~;](https://static.techno-science.net/illustration/Definitions/autres/b/b04174f2fc4db1ab25cb854482a085dc_6c969452c27cb7bc931e3f0d310b926d.png)