Algèbre des parties d'un ensemble - Définition
La liste des auteurs de cet article est disponible ici.
Intersection
Définition
Pour tout ensemble A et tout ensemble B, il existe un ensemble S dont les éléments sont ceux qui sont communs à A et à B. Cette proposition, qui est un axiome implicite de la théorie naïve des ensembles, découle, dans la théorie des ensembles, du schéma d'axiomes de compréhension. En notation symbolique :
L'unicité de l'ensemble S est garantie par l'axiome d'extensionnalité. On le note « A ∩ B » ( lire « A inter B » ), et on l'appelle intersection de A et de B.
Propriétés
Pour tous ensembles A, B, C, D, on a les propriétés suivantes :
- N1 (commutativité) : l'intersection de deux ensembles ne dépend pas de l'ordre dans lequel ces deux ensembles sont pris :
- N2 (Ø absorbant) : l'intersection de l'ensemble vide et d'un ensemble quelconque est vide :
- N3 (idempotence) : l'intersection d'un ensemble quelconque avec lui-même redonne cet ensemble :
- N4 : l'intersection de deux ensembles est incluse dans chacun de ces deux ensembles :
- N5 : un ensemble A est inclus dans un ensemble B si et seulement si leur intersection est égale à A :
- N6 : l'équivalent de U6 se traduit par une définition, celle des ensembles disjoints (voir ci-dessous).
- N7 (compatibilité avec l'inclusion) : l'intersection de deux sous-ensembles est incluse dans l'intersection des deux ensembles dont ils sont sous-ensembles :
- N8 (associativité) : le résultat de l'intersection de plusieurs ensembles ne dépend pas de l'ordre dans lequel les opérations sont faites :
Cas des familles d'ensembles
Il est possible de définir l'intersection d'une famille quelconque d'ensembles
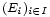
-
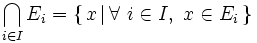
En particulier, pour une famille vide d'ensembles,
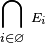
Ensembles disjoints
Deux ensembles sont disjoints si et seulement si leur intersection est vide, c'est-à-dire s'ils n'ont pas d'éléments en commun. Par exemple, si A = { 1, 2 } et B = { 3, 4 }, alors A ∩B = Ø, et A et B sont donc disjoints.
Il existe deux manières de généraliser cette définition à plus de deux ensembles : E désignant un ensemble d'ensembles,
- les éléments de E sont dits (globalement) disjoints si « l'ensemble noyau de E » (noté ∩E et désignant l'intersection de tous les ensembles appartenant à E) est vide :
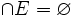
- les éléments de E sont dits mutuellement disjoints ou disjoints deux à deux si et seulement si l'ensemble noyau de toute paire de ces éléments est vide, c'est-à-dire si :
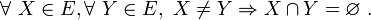
Ces deux notions sont différentes : des ensembles disjoints deux à deux sont globalement disjoints (dès qu'il y en a au moins deux), tandis que des ensembles globalement disjoints ne le sont pas nécessairement deux à deux.
Liens avec la réunion
Pour tous ensembles A, B, C, on a les deux propriétés suivantes :
- UN1 (distributivité de l'intersection par rapport à la réunion : l'intersection de la réunion de deux ensembles avec un troisième ensemble est égale à la réunion de l'intersection de chacun des deux premiers ensembles avec le troisième :
- UN2 (distributivité de la réunion par rapport à l'intersection) : la réunion de l'intersection de deux ensembles avec un troisième ensemble est égale à l'intersection de la réunion de chacun des deux premiers ensembles avec le troisième :
De chaque côté de l'égalité (UN1) figure un ensemble et nous voulons démontrer que ces ensembles sont égaux, c'est-à-dire montrer qu'un élément quelconque x appartient au premier si et seulement s'il appartient au second. Notons respectivement a, b, c les propositions
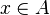
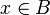
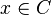
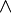
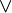
ce qui traduit exactement l'équivalence souhaitée :
La démonstration de (UN2) est identique, en échangeant
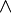
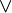
![\exist S,~\forall x,~(x\in S)\Leftrightarrow[(x\in A)\land(x\in B)]~.](https://static.techno-science.net/illustration/Definitions/autres/d/d451ca24efe83db9e228ddfd45350c54_fadf158cdd9cf7f8921f661c673a626c.png)
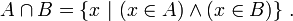
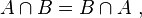
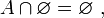
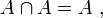
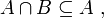
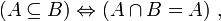
![[(A\subseteq B)\land(C\subseteq D)]\Rightarrow[(A\cap C)\subseteq(B\cap D)]~,](https://static.techno-science.net/illustration/Definitions/autres/d/d02c77cf70e6d51db83587d27cb7e9b3_d9d5d7288738e0f9ab7afd2412a8af38.png)
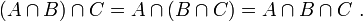
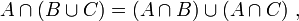
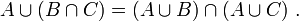
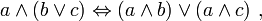
![x\in[A\cap(B\cup C)]\Leftrightarrow x\in[(A\cap B)\cup(A\cap C)]~.](https://static.techno-science.net/illustration/Definitions/autres/2/2b1124f6fc9430b6be7305e01d74884c_bf4693dad043c2207f57204c99a2e9bb.png)

















































