Algorithmes de remplacement des lignes de cache - Définition

Introduction

Il existe différents types de mémoire cache, dont l'organisation amène des situations où une ligne de la mémoire principale est mappé sur un ensemble de lignes de mémoire cache remplie. Il faut donc choisir la ligne de mémoire cache qui sera remplacée par la nouvelle ligne. Cette sélection est réalisée par les algorithmes de remplacement de lignes de cache. Le principe de fonctionnement de la majorité de ces algorithmes repose sur le principe de localité. Ces algorithmes sont en général divisés en deux grandes catégories :

• les algorithmes dépendants de l'utilisation des données: , , etc…
• les algorithmes indépendants de l'utilisation des données : , .

Algorithme optimal

Cet algorithme, formalisé par L.A. Belady, utilise la mémoire cache de manière optimale : il remplace la ligne de mémoire cache qui ne sera pas utilisée pour la plus grande période de temps. Par conséquent, cet algorithme doit connaître les accès futurs afin de désigner la ligne à évincer. Cela est donc impossible à réaliser dans un système réel mais constitue néanmoins un excellent moyen afin de mesurer l'efficacité d'un algorithme de remplacement en fournissant une référence.

Approximations de l'algorithme LRU

En raison de la complexité d'implémentation de l'algorithme LRU, qui influe de manière négative sur le temps moyen d'accès à la mémoire cache, des approximations de l'algorithme LRU ont été développées afin de pallier ces problèmes. Les différents algorithmes présentés dans cette section utilisent toutes le fait que dans le bas de la liste d'accès, la probabilité que le processeur requiert une de ces lignes est quasiment identique. Par conséquent, désigner une de ces lignes pour l'éviction donne des résultats très proches. Un ordre partiel à l'intérieur de ces ensembles est donc suffisant.

Toutes les figures dessinées ici respectent la convention suivante : le vert correspond à des lignes protégées de l'éviction et le jaune aux lignes considérées comme LRU.

PLRUt (Arbre de décision binaire)

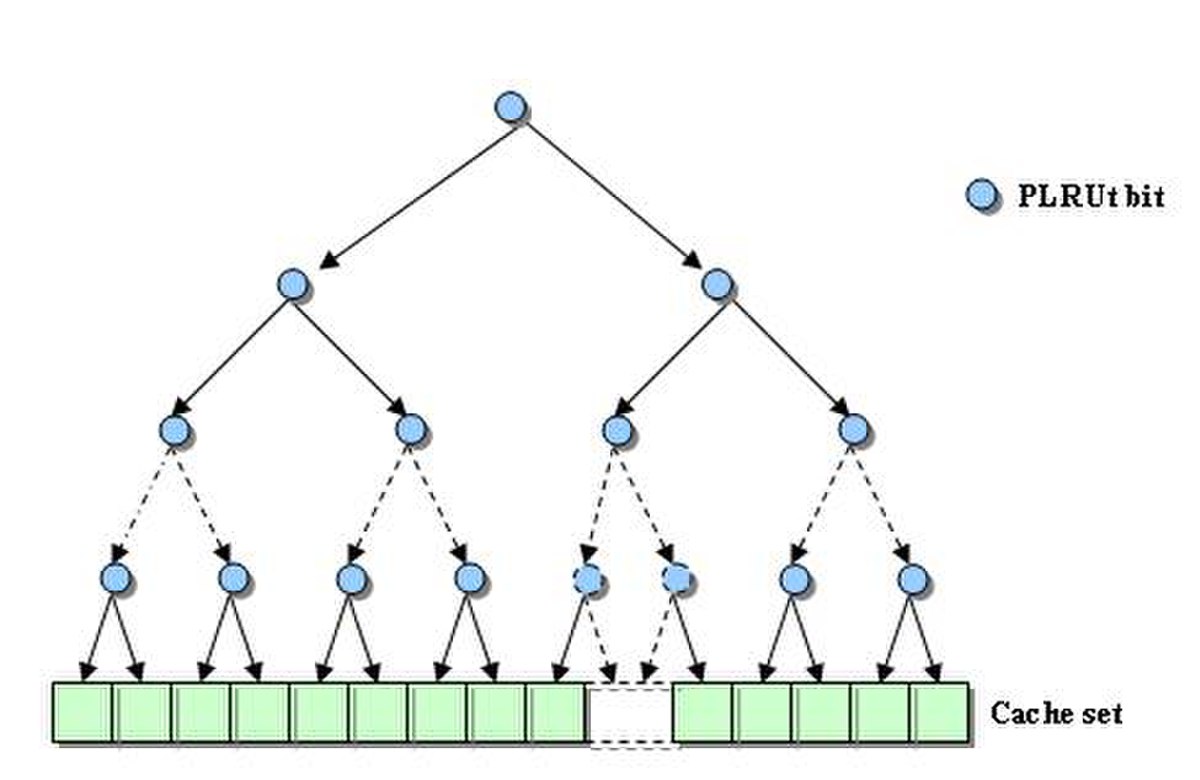
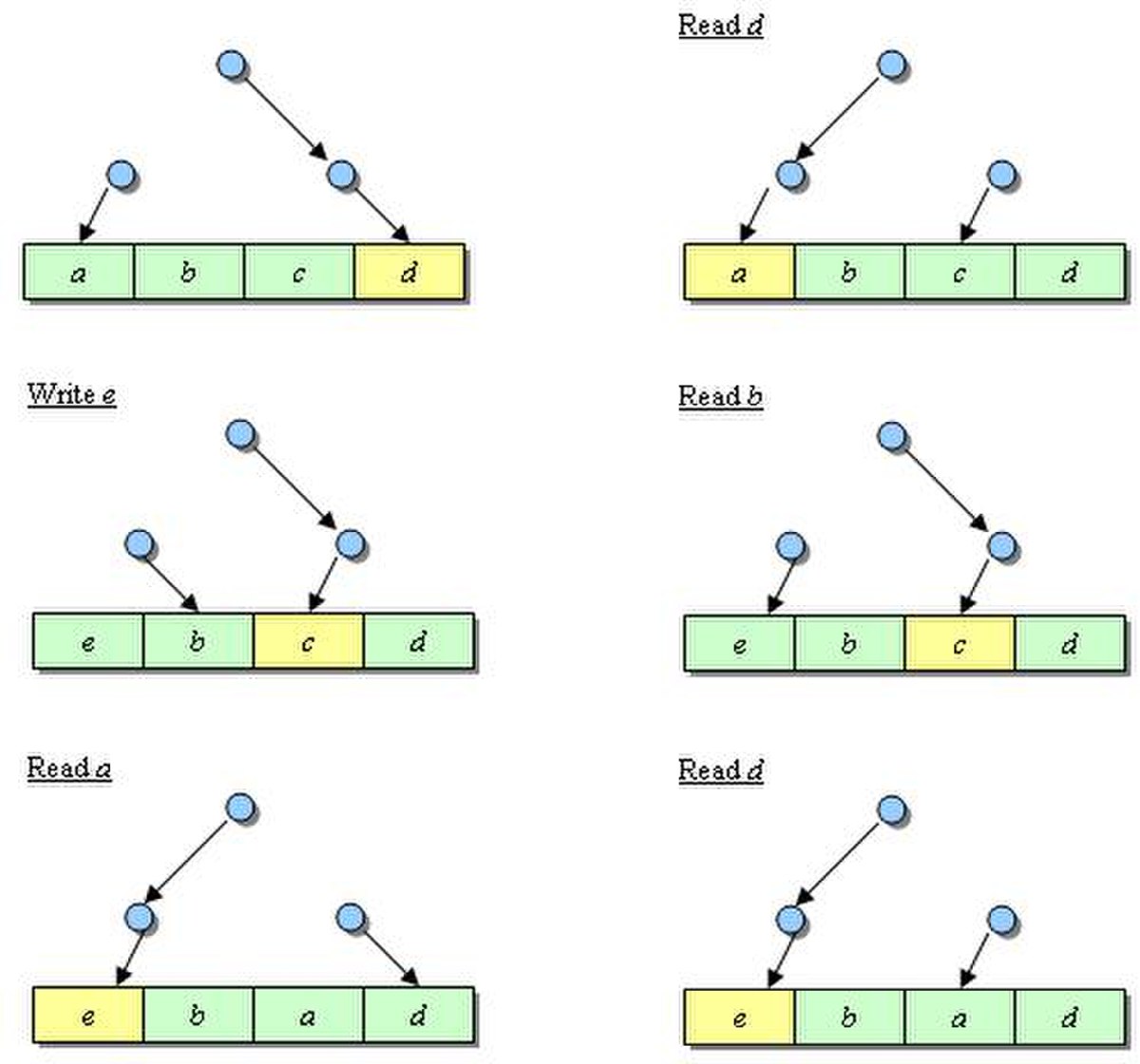
La première approximation est fondée sur un arbre de décision binaire. Elle ne requiert que N-1 bits par ensemble dans un cache associatif de N voies. Ces différents bits pointent la ligne considérée comme pseudo-LRU. Les bits de l'arbre de décision binaire pointant sur la voie hitée sont inversés pour protéger cette ligne de l'éviction. Prenons l'exemple d'un cache de 4 voies représenté sur la figure ci-dessous. Chaque dessin correspond au résultat de l'accès mémoire présenté.

La nature binaire de cet algorithme est également la faiblesse de l'algorithme : le nœud en haut de l'arbre binaire ne contient qu'une information et ne peut donc pas refléter suffisamment bien l'histoire des différentes voies.

Arbre de décision binaire de PLRUt

Séquence avec l'algorithme PLRUt

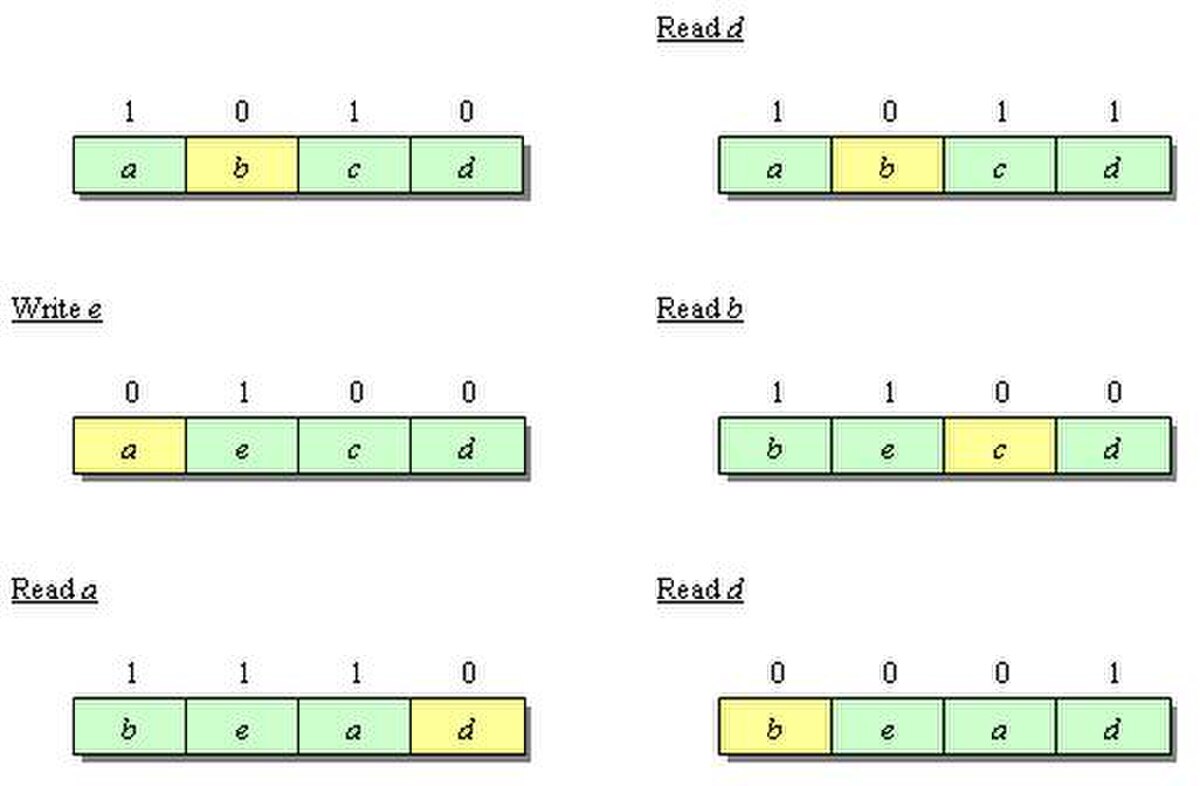
PLRUm

À chaque ligne de mémoire cache est assigné un bit. Lorsqu'une ligne est écrite, son bit est mis à 1. Si tous les bits d'un ensemble sont égaux à 1, tous les bits sauf le dernier sont réinitialisés à zéro. Cet algorithme est populaire dans de nombreux caches. Selon Al-Zoubi et al., ces deux pseudo-algorithmes sont de très bonnes approximations et PLRUm donne même de meilleurs résultats que LRU sur certains algorithmes.

Séquence avec l'algorithme PLRUm

1-bit

C'est probablement la plus simple des approximations de l'algorithme LRU et ne requiert qu'un bit par ensemble. Ce bit partage l'ensemble en deux groupes :

• l'un qui contient le MRU (Most Recently Used)
• l'autre non.

Lors d'un hit ou d'un défaut de cache, ce bit est réévalué pour pointer sur la moitié qui ne contient pas le MRU. La ligne à remplacer est ensuité choisie au hasard parmi ce groupe.