Arbre de Stern-Brocot - Définition

Déplacement dans l'arbre

Idée

Étant donné qu'un rationnel n'apparait qu'une et une seule fois dans l'arbre, alors on peut considérer cet arbre comme un pur système de numération. Prenons la suite des pas que l'on va faire dans l'arbre pour atteindre la fraction souhaité. On définit donc deux "pas" : le pas G (gauche) et le pas D (droite) (dans le livre cité en référence on a L et R mais pour des raisons évidentes de traduction, on mettra G et D). On peut donc représenter tout rationnel positif comme une unique suite de G et D qui représente son chemin dans l'arbre.

Prenons un exemple : considérons le mot GDDG, on part de 1/1 pour arriver à 1/2, puis on va à droite vers 2/3, encore à droite, 3/4, et enfin à gauche 5/7.

On remarque que l'on doit partir de 1/1 (pour avoir un point de départ bien fixé et on suppose que 0 n'est jamais demandé). Convenons pour l'instant de l'appeler "Identité".

Mais comment trouver de façon simple une fraction à partir d'un mot composé de G et de D.

Représentation matricielle

Soit un mot S composé de G et de D, on définit f(S) comme la fraction correspondant à S.

On aimerait trouver un moyen simple pour exprimer f.

Pour cela on va partir d'une représentation matricielle. Si vous ne comprenez pas les calculs ci-dessous, reportez vous à l'article sur les matrices. La théorie pure des matrices n'est pas vraiment utile ici, mais le calcul l'est, cela ne requiert donc aucun niveau d'algèbre linéaire.

On identifiera dans la suite la fraction à la matrice colonne . Étant donné une telle matrice colonne, on notera le rationnel associé. Étant donné deux matrices colonnes V₁ et V₂, leur médian est V₁ + V₂. De façon matricielle, si on définit M comme la matrice 2x2 constituée des deux blocs V₁ et V₂, leur médian est tout simplement .

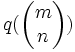
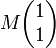
Remarquons maintenant que chaque élément V de l'arbre de Stern-Brocot est associé de façon unique aux deux éléments de l'arbre V₁ et V₂ à partir desquels il a été obtenu lors de la construction de l'arbre avec q(V₁) < q(V₂). On note gen(V) la matrice par blocs .

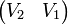
Pour calculer f(S), l'idée est alors de calculer récursivement gen(f(S)), qu'on notera

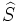
On remarque tout d'abord (où ε représente le mot vide et I est la matrice identité).

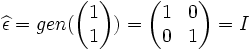
Si , on a .

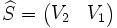
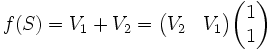
D'où :

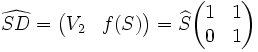
et :

On peut alors définir deux matrices : .

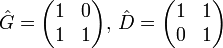
Ainsi, on a une façon très agréable de calculer notre fraction puisque si S est le mot , on a et .

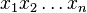
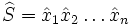
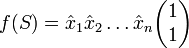
Reprenons l'exemple cité précédemment :

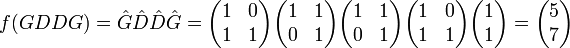
Réciproque / Algorithmes

Pour la réciproque, c’est-à-dire, pour trouver le chemin effectué pour atteindre une fraction quelconque m / n il faut utiliser le Théorème de Bezout : si on suppose que m / n est irréductible, c'est à dire que m et n sont premiers entre eux, alors il existe deux entiers m' et n' tels que mn' − m'n = 1; si de plus on suppose que m et n sont distincts et tous les deux non nuls, alors on peut choisir m' et n' de façon que et 0 < n' < n (les coefficients m' et n' satisfaisant toutes ces contraintes sont directement calculés par l'algorithme d'Euclide étendu). Dans ce cas les fractions m' / n' et m / n sont consécutives dans la suite de Farey d'ordre n.

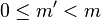
On pose alors m'' = m − m' et n'' = n − n' ; par construction m / n est le médian de m' / n' et m'' / n'' et on a m' / n' < m / n < m'' / n''. Dans l'arbre de Stern-Brocot, la fraction m / n est la fille de celle des deux fractions m' / n' et m'' / n'' qui a le plus grand dénominateur, c'est à dire la fille droite de m' / n' si n' > n'', ou la fille gauche de m'' / n'' si au contraire n' < n''.

Par exemple si on considère la fraction 5 / 7 alors l'algorithme de d'Euclide nous donne . On en déduit que 2 / 3 et (5 − 2) / (7 − 3) = 3 / 4 sont les voisines de 5 / 7 dans la suite de Farey d'ordre 7; comme 4 > 3, on a que 5 / 7 est la fille de gauche de 3 / 4 dans l'arbre de Stern-Brocot.