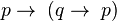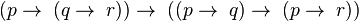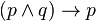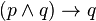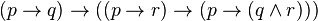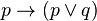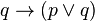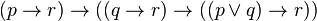Calcul des propositions - Définition

Logique classique, minimale, intuitionniste

Les axiomes et règles du calcul propositionnel que nous avons présentés sont ceux de la logique classique. Ils induisent la proposition p ∨ ¬p, appelée principe du tiers exclu, la proposition ¬¬ p → p, appelée élimination de la double négation et la proposition ((p → q) → p) → p appelée loi de Peirce. Cette logique repose sur le principe qu'une propriété P est nécessairement vraie ou fausse. Il est l'un des piliers de la position qualifiée de formaliste, adoptée par Hilbert et d'autres. Or cette position qui implique qu'il y a des démonstrations qui ne construisent pas l'objet satisfaisant la proposition prouvée a été remise en cause par plusieurs mathématiciens, dont le plus connu est Brouwer conduisant à créer par la suite la logique intuitionniste.

Nous présentons maintenant deux variantes très proches de logique non classique, la logique minimale de I. Johansson (1936) et la logique intuitionniste de Heyting (1930). Les connecteurs primitifs sont →, ∧, ∨ et ¬. On garde les deux premiers axiomes de la logique classique :

Avant d'introduire la négation, on énonce les axiomes relatifs à  :

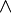
et ceux relatifs à , (duaux des précédents) :

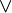
On introduit enfin deux axiomes relatifs à la négation. Le premier exprime que, si f implique sa propre négation, alors f est invalide.

(p → ¬p) → ¬p.

Le second définit le comportement de chaque logique vis-à-vis d'une contradiction et la seule différence entre la logique minimale et la logique intuitionniste porte sur cet axiome.

¬p → (p → ¬q) pour la logique minimale et ¬p → (p → q) pour la logique intuitionniste.

En présence d'une proposition et de sa négation, les trois logiques, classique, intuitionniste et minimale, concluent toutes trois à une contradiction ⊥. Mais la différence porte sur l'utilisation que l'on fait de cette contradiction :

• La logique classique déduit de ¬P → ⊥ le fait que P est vrai (raisonnement par l'absurde).
• La logique intuitionniste déduit d'une contradiction que toute proposition est démontrable. De ¬P → ⊥, elle déduit la validité de ¬¬P, propriété plus faible que P.
• La logique minimale déduit d'une contradiction que toute négation de proposition est démontrable, ce qui est plus faible que ce que propose la logique intuitionniste.

Logique minimale et logique intuitionniste ont toutes deux la proposition ¬(p ∧ ¬p) comme théorème. En revanche, p ∨ ¬p n'est pas un théorème de ces logiques.

De même, elles permettent de démontrer p → ¬¬p mais pas la réciproque. Par contre, elles permettent de démontrer l'équivalence entre ¬p et ¬¬¬p. Enfin, la proposition (¬p ∨ q) → (p →q) est un théorème de la logique intuitionniste, mais pas un théorème de la logique minimale.

Glivenko a démontré en 1929 que p est un théorème du calcul propositionnel classique si et seulement si ¬¬p est un théorème du calcul propositionnel intuitionniste. Ce résultat ne s'étend pas si l'on remplace « intuitionniste » par « minimal ». Il ne s'applique pas non plus au calcul des prédicats ; une traduction est toutefois possible, mais dépend de la structure des formules.