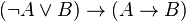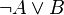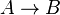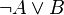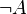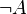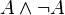Logique minimale - Définition

Introduction

La logique minimale est, comme la logique intuitionniste, une variante de la logique classique. Les trois logiques diffèrent sur la façon de traiter la négation et la contradiction dans le calcul des propositions ou le calcul des prédicats. Dans une certaine mesure, la logique minimale n'aborde pas ce concept et représente une logique sans véritable négation.

Comparaison entre les diverses logiques

On utisera comme notation les symboles suivants : pour la disjonction, pour la conjonction, pour l'implication, pour la négation, pour l'équivalence.

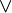
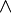
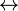
Les règles communes

Dans les trois logiques, on dispose des deux règles suivantes, relatives à la négation :

• La règle d'élimination de la négation : Si on a à la fois une proposition A et sa négation , alors on a une contradiction, notée .
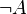
• La règle d'introduction de la négation : Si une proposition A conduit à une contradiction, alors c'est que est valide. Cette règle peut d'ailleurs être prise comme définition de la négation : est un synonyme de .

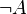
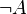
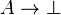
Les différences

Les trois logiques diffèrent sur les conséquences à tirer d'une contradiction.

• La logique classique utilise le raisonnement par l'absurde et déduit de le fait que A est valide. C'est en fait une règle d'élimination de la double négation, puisque est un synonyme de .
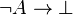
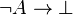
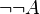
• La logique intuitionniste déduit d'une contradiction n'importe quelle proposition : , ce qu'on résume par la formule ex falso sequitur quodlibet.
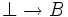
• La logique minimale ne prévoit aucun traitement lié à .

Il en résulte que la logique minimale n'établit pas de différence entre la formule et n'importe quelle autre formule. Considérons par exemple une formule quelconque C. Définissons comme synonyme de . On a alors :

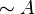
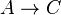
• Si on a à la fois A et , alors on a C. En effet, de A et de , on peut déduire C. C'est la règle du modus ponens.
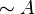
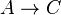
• Si une proposition A conduit à C, alors on a et donc .

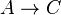
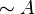
On voit donc que, si on n'attribue aucun rôle particulier à la contradiction, on peut faire jouer le rôle de cette contradiction à n'importe quelle formule C, en définissant la négation comme étant , et qu'inversement, on peut supprimer toute référence à la négation en logique minimale.

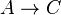
Par souci de comparaison avec les autres logiques, nous continuerons néanmoins à utiliser les symboles et

Exemples de formules valides en logique minimale

Exemple 1 :

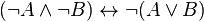
En effet, supposons qu'on ait (autrement dit, on a à la fois et ). Montrons que l'on a , autrement dit, montrons que l'hypothèse conduit à une contradiction. Distinguons les cas : soit on a A qui est bien contradictoire avec l'hypothèse , ou bien on a B qui est contradictoire avec . Dans tous les cas, on a une contradiction, CQFD.

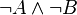
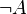
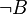
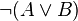
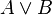
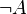
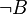
Réciproquement, supposons que l'on ait et montrons que l'on a , autrement dit que A conduit à une contradiction. Mais A entraîne qui est contradictoire avec l'hypothèse. CQFD. On procède de même pour montrer .

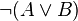
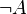
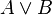
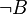
Par contre, on a seulement , la réciproque étant seulement vraie en logique classique.

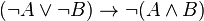
Exemple 2 :

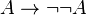
Supposons qu'on ait A. Alors l'hypothèse supplémentaire conduit à une contradiction. On a donc . CQFD

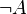
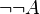
La réciproque est invalide en logique minimale et en logique intuitionniste. On dispose cependant de . En effet, supposons que . L'hypothèse supplémentaire A entraîne qui est contradictoire avec , donc on a .

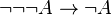
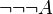
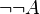
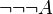
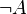
Exemple 3 : On peut montrer la validité en logique minimale de . Mais la réciproque est seulement valide en logique intuitionniste ou en logique classique.

Exemple 4 : En ce qui concerne la contraposition, on peut montrer qu'en logique minimale, on a , ainsi que et , mais on ne dispose pas de qui est une variante du raisonnement par l'absurde.

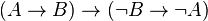
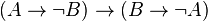
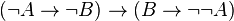
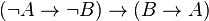
Exemples de formules invalides

Exemple 1 : La formule est invalide en logique minimale. En effet, si elle était prouvable, alors on pourrait prouver également, en remplaçant par une proposition quelconque C que , or cette dernière formule n'est pas même prouvable en logique classique, sans hypothèse supplémentaire sur C.

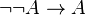
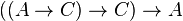
Exemple 2 : La formule est valide en logique intuitionniste et en logique classique, mais pas en logique minimale. En effet, une preuve demanderait de supposer et d'en déduire , et donc de supposer A et d'en déduire B. L'utilisation de par disjonction des cas et de A pour prouver B demanderait de prouver que et A prouvent B, et que B et A prouvent B. Mais la preuve de B à partir de et A n'existe pas en logique minimale. Elle existe en logique intuitionniste, puisque, de la contradiction , on peut déduire B.