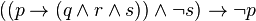Calcul des propositions - Définition
La liste des auteurs de cet article est disponible ici.
Principales propriétés
Le calcul propositionnel dispose donc de plusieurs moyens différents pour « valider » les propositions : les systèmes de déduction qui démontrent les théorèmes et les méthodes sémantiques qui définissent les tautologies. La question qui se pose est de savoir si ces méthodes coïncident.
Décidabilité, cohérence, complétude, compacité
Le fait que toute proposition soit démontrable si et seulement si elle est une tautologie exprime une propriété du calcul propositionnel que l'on appelle la complétude, cela signifie que la présentation déductive du calcul propositionnel est équivalente à la présentation sémantique. La complétude repose sur les remarques suivantes.
- Toute proposition démontrée résulte d'un axiome ou de l'application d'une règle sur des propositions déjà démontrées. Or il est facile de vérifier que les axiomes fournissent des tautologies et que les règles conservent les tautologies. Toute proposition démontrée est donc une tautologie. Le calcul propositionnel est correct.
- La réciproque repose sur le fait suivant: on peut démontrer que pour toute proposition P du calcul propositionnel il existe une proposition P' telle que
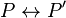
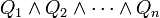
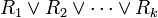
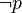
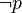
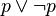
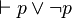
L'article théorème de complétude du calcul des propositions propose une autre démonstration plus détaillée.
Il résulte de la complétude du calcul des propositions que :
- Le calcul des propositions est décidable, dans le sens où il existe un algorithme permettant de décider si une proposition est un théorème ou non. Il suffit de dresser sa table de vérité et de voir s'il s'agit d'une tautologie.
- Le calcul des propositions est cohérent (consistant), c'est-à-dire non contradictoire. Il n'existe aucune proposition P telle qu'on puisse avoir en même temps
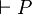
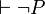
- Le calcul des propositions est fortement complet (maximalement cohérent), dans le sens où tout ajout d'un nouveau schéma d'axiome, non démontrable dans le système initial, rend ce système incohérent.
Supposons donné un nombre infini de propositions. Peut-on satisfaire simultanément ces propositions ? Autrement dit, existe-il des valeurs de vérité pour leurs variables propositionnelles qui donnent 1 comme valeur de vérité à toutes les propositions? Si la réponse est positive pour tout sous-ensemble fini de ces propositions, alors elle l'est pour toutes les propositions. Cette propriété, qui assure que l'on peut passer de tous les sous-ensembles finis à l'ensemble infini tout entier, est appelée la compacité.
Méthodes de calcul, NP-complétude
Nous avons vu que, pour décider si une proposition est démontrable, il suffit de vérifier si c'est une tautologie, c'est-à-dire de vérifier si elle prend la valeur de vérité 1 quelles que soient les valeurs de vérité de ses variables propositionnelles.
Cette approche brutale se heurte cependant au temps de calcul qu'elle requiert. En effet, si la proposition possède n variables propositionnelles, il faut calculer 2n combinaisons de valeurs possibles pour les variables propositionnelles, ce qui devient rapidement infaisable pour n grand. Ainsi, si n = 30, il faudra énumérer plus d'un milliard de combinaisons de valeurs.
Il existe certes des améliorations possibles. Par exemple, si on attribue la valeur de vérité 0 à une variable propositionnelle p, on peut attribuer directement la valeur 0 à
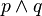
On peut également chercher à voir s'il est possible d'invalider les implications. Considérons par exemple la proposition :
Étant constituée d'une implication, pour la rendre invalide, il suffit que la conclusion
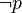
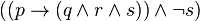
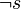
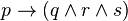
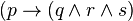
Mais les améliorations précédentes ne changent pas fondamentalement la difficulté du problème. On est donc devant la situation suivante. Étant donnée une proposition f, on se demande si f est une tautologie ou non et pour cela, on se demande s'il existe des valeurs de vérité attribuables aux variables propositionnelles de f qui rendraient f invalide.
- Une recherche exhaustive demande 2n vérifications si f possède n variables propositionnelles. Cette démarche est dite déterministe, mais son temps de calcul est exponentiel.
- Par contre, si f n'est pas une tautologie, il suffit d'une vérification à faire, à savoir tester précisément la configuration qui invalide f. Cette vérification demande un simple calcul booléen, qui se fait en temps polynomial (essentiellement linéaire en fait). Le temps de calcul cesse donc d'être exponentiel, à condition de savoir quelle configuration tester. Celle-ci pourrait par exemple être donnée par un être omniscient auquel on ne ferait pas totalement confiance. Une telle démarche est dite non [déterministe|Machine_de_Turing_non_déterministe].
La question de l'invalidité de f, ainsi que tous les problèmes qui se résolvent suivant la méthode que nous venons d'esquisser, sont dits NP (pour polynomial non déterministe). Tester l'invalidité de f équivaut par des calculs très simples (en temps polynomial) à tester la satisfaisabilité de sa négation. Le problème de la satisfaisabilité d'une proposition, à savoir trouver une configuration qui donne 1 comme valeur de vérité de la proposition est appelé problème SAT. Il joue un rôle fondamental en théorie de la complexité, puisqu'on peut montrer que la découverte d'un algorithme déterministe en temps polynomial pour ce problème permettrait d'en déduire des algorithmes déterministes en temps polynomial pour tous les problèmes de type NP (théorème de Cook). On dit que SAT (et donc également le problème de la non-démontrabilité d'une proposition) est un problème NP-complet. Le problème de la démontrabilité d'une proposition est dit co-NP (pour complémentaire de NP).
Le problème SAT désigne en fait le plus souvent celui de la satisfaisabilité d'une conjonction de clauses (un cas particulier parmi les propositions), mais on ramène le problème de la satisfaisabilité d'une proposition à celui-ci par une réduction polynomiale (une mise sous forme clausale par équisatisfaisabilité, celles par équivalence logique ne fonctionnent pas).
Algèbre de Boole
Soit E l'ensemble des propositions sur un ensemble de variables propositionnelles. La relation binaire définie sur E par l'équivalence entre deux propositions est notée ≡. C'est une relation d'équivalence sur E, compatible avec la conjonction (qui donne la borne supérieure de deux éléments), la disjonction (qui donne la borne supérieure de deux éléments), et la négation (qui donne le complément). L'ensemble quotient E/≡ du calcul propositionnel.
Dès que l'ensemble des variables propositionnelles est infini, l'algèbre de Lindenbaum des formules propositionnelles ne possède aucun atome, c'est-à-dire aucun élément non nul minimal (pour toute formule qi n'est pas une antilogie, on obtient un élément strictement inférieur par conjonction avec une variable propositionnelle non présente dans la formule). Ceci la distingue de l'algèbre de Boole de toutes les parties d'un ensemble, qui a pour atomes les singletons de celui-ci.
Formes normales conjonctives, formes normales disjonctives
Une disjonction est une proposition de la forme
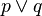
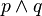
Exemples :
-
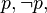
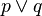
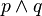
-
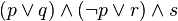
-
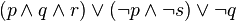
Lorsque chaque bloc disjonctif d'une FND comporte une et une seule occurrence des mêmes variables propositionnelles, on parle alors de FND distinguée.
Lorsque chaque bloc conjonctif d'une FNC comporte une et une seule occurrence des mêmes variables propositionnelles, on parle alors de FNC distinguée.
Exemples :
-
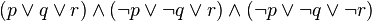
-
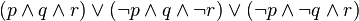
On peut montrer que toute proposition est équivalente à une FND (en admettant que