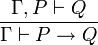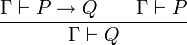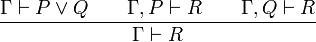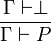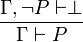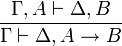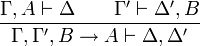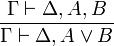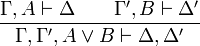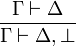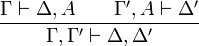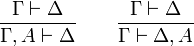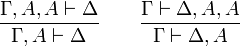Calcul des propositions - Définition

Présentation

Syntaxe

Les constituants du langage

À la base de la syntaxe du calcul des propositions sont les variables propositionnelles ou propositions atomiques, notées p, q, etc., formant un ensemble infini dénombrable.

Les deuxièmes constituants de base du langage du calcul des propositions sont les opérateurs ou connecteurs. Ce sont des symboles qui permettent de construire des propositions plus élaborées. Les plus courants de ces connecteurs logiques sont et ∧, ou ∨, non ¬, implique → ou ⇒, équivaut ↔ ou ⇔. On considère souvent aussi la constante ⊥ qui vise à représenter le faux.

À côté de ces symboles on utilise des parenthèses pour lever les ambiguïtés dans les formules (choix adopté ci-dessous), ou une notation comme la notation polonaise, inventée par le logicien polonais Jan Łukasiewicz. Il est important que la définition des formules soit simple et sans ambiguïtés, pour permettre en particulier les définitions inductives sur la structure des formules, mais pratiquement il est possible d'économiser les parenthèses, soit en adoptant certaines conventions pour lever les ambiguïtés, soit parce que le contexte fait que ces ambiguïtés sont sans importance.

Les formules propositionnelles

Le calcul des propositions repose de plus sur des règles de formation indiquant comment construire des propositions complexes à partir des propositions élémentaires, ou atomes, que sont les variables propositionnelles, et d'éventuelles constantes comme ⊥. Ces règles déterminent quels assemblages de signes, quels mots, sont bien formés et désignent des propositions. La définition dépend d'un choix de connecteurs, et d'un choix d'atomes.

On se donne un ensemble de variables propositionnelles. L'ensemble des formules du calcul des proposition (sur ), ou simplement des propositions, est défini par induction, c'est-à-dire que c'est le plus petit ensemble tel que :

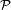
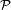
• une variable propositionnelle p de est une formule ;
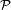
• ⊥ est une formule ;
• si P et Q sont des formules, alors (P ∧ Q), (P ∨ Q), (P → Q), (P ↔ Q) et ¬P sont des propositions.

Exemples : Si P, Q et R sont des propositions,

(P → Q) → (¬Q → ¬P) est une proposition.

(P → ⊥) → ⊥ est une proposition.

P ∧ ¬P est une proposition.

(P ∧ Q) ∨ R est une proposition.

P ∧ Q ∨ n'est pas une proposition.

Quelques conventions syntaxiques

Afin d'alléger la présentation des expressions sans mettre en péril l'absence d'ambiguïté, on autorise par des conventions syntaxiques certaines entorses à la définition ci-dessus.

• On omet généralement les parenthèses extrêmes des formules.

• On supprime souvent les parenthèses en associant les expressions de droite à gauche quand il s'agit du même connecteur : A ∧ B ∧ C pour ((A ∧ B) ∧ C)

Pour la lisibilité, on utilise également plusieurs formes de parenthèses (taille, remplacement par des crochets, ...)

Par ailleurs, on démontre que seules les parenthèses ouvrantes sont nécessaires à la non-ambiguïté de la lecture des formules qui pour cette raison sont remplacées par un point "." dans certaines notations.

Les systèmes déductifs

Le calcul des propositions permet de présenter les trois systèmes déductifs les plus connus. On se limite pour cela aux propositions contenant, outre les variables propositionnelles, seulement des implications, des disjonctions et des occurrence de faux autrement dit de ⊥. On admet que ¬P est une abréviation de P → ⊥. Si P est un théorème, autrement dit une proposition qui a une démonstration, on note cela par P.

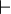
Les systèmes déductifs utilisent des règles de déduction (appelées aussi règles d'inférence) qui s'écrivent:

Les sont appelées les prémisses et ψ est appelée la conclusion.

La déduction à la Hilbert

Il n'y a qu'une seule règle appelée le modus ponens, elle s'écrit:

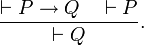
Elle peut se comprendre ainsi si est un théorème et P est un théorème alors Q est un théorème. À cela, on peut ajouter trois axiomes pour l'implication et le faux et trois axiomes pour la disjonction:

• ,
• ,
• ,
• ,
• ,
• .

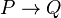
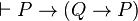
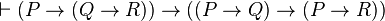
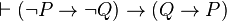
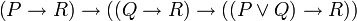
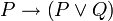
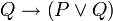
La déduction naturelle

Alors que la déduction à la Hilbert manipule et démontre des théorèmes, la déduction naturelle démontre des propositions sous des hypothèses et quand il n'y a pas (plus) d'hypothèses, ce sont des théorèmes. Pour dire qu'une proposition P est conséquence d'un ensemble Γ d'hypothèses, on écrit . Alors que dans la déduction à la Hilbert, il n'y a qu'une règle et plusieurs axiomes, dans la déduction naturelle il y a un seul axiome et plusieurs règles. Pour chaque connecteur, on classe les règles en règles d'introduction et en règles d'élimination.

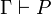
• L'axiome est .
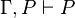
• La règle d'introduction de l'implication:

• La règle d'élimination de l'implication:

• Les deux règles d'introduction de la disjonction, droite et gauche:

• La règle d'élimination de la disjonction:

• La règle d'élimination du faux:

En outre, il faut une règle qui est la réduction à l'absurde, nécessaire en logique classique:

On remarquera que la règle d'élimination de l'implication est très proche du modus ponens, d'ailleurs on l'appelle aussi modus ponens. On remarquera qu'il n'y pas de règle d'introduction du faux et que la règle d'élimination du faux revient à dire que si d'un ensemble d'hypothèses je déduis le faux (ou l'absurde) alors de ce même ensemble je peux déduire n'importe quoi. On remarquera que la réduction à l'absurde est la règle qui correspond au raisonnement par l'absurde: pour démontrer P, on ajoute aux hypothèses et si l'on obtient l'absurde, alors on a P.

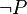
Le calcul des séquents

L'une des idées qui à conduit au calcul des séquents est de n'avoir plus que des règles d'introduction en plus d'une règle que l'on appelle coupure et de règles structurelles. Pour cela, on utilise des formules que l'on appelle des séquents et qui sont de la forme où Γ et Δ sont des multiensembles de propositions. Le séquent s'interprète comme l'assertion de la conjonction des P_i on déduit la disjonction des Q_j. Les P_i sont appelés les antécédents et les Q_j sont appelés les conséquents. Si la liste des antécédents est vide on écrit , si la liste des conséquents est vide on écrit . Un théorème est encore un séquent sans antécédents et avec un seul conséquent.

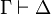
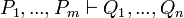
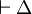
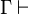
• L'axiome est .

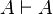
• Introduction de l'implication à droite :

• Introduction de l'implication à gauche :

• Introduction de la disjonction à droite :

• Introduction de la disjonction à gauche :

• Introduction du faux à droite :

• Introduction du faux à gauche, il a la forme d'un axiome :

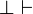
• Coupure :

• Affaiblissements :

• Contractions

Une coupure traduit l'attitude du mathématicien qui démontre un lemme (la proposition A) dont il se sert ailleurs dans la démonstration d'un théorème. Ce lemme peut exprimer quelque chose qui n'a rien à voir avec le théorème principal, d'où le souhait d'éliminer ces lemmes qui sont comme des détours dans la progression vers le résultat principal. Un affaiblissement correspond à l'ajout d'une proposition superflue soit comme antécédent, soit comme conséquent.

Exemples de théorèmes

Nous indiquons ci-dessous une liste de théorèmes qu'on peut démontrer à l'aide des règles précédentes, ainsi que le nom usuel qui leur est attribué par la tradition.

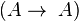
	identité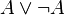
	tiers exclu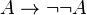
	double négation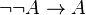
	double négation classique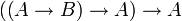
	loi de Peirce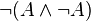
	non contradiction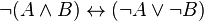
	lois de De Morgan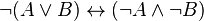
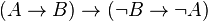
	contraposition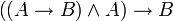
	modus ponens (propositionnel)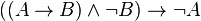
	modus tollens (propositionnel)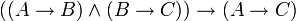
	modus barbara (propositionnel)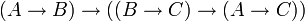
	modus barbara (implicatif)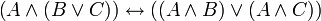
	distributivité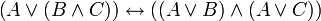

Commentaires

On aura remarqué que les trois systèmes utilisent le même symbole , mais en fait cette notation est cohérente. Le format utilisé pour la déduction naturelle est en fait un séquent dans lequel il n'y a qu'une seule conclusion, on parle alors d'un séquent naturel. Le format utilisé pour les théorèmes dans les systèmes à la Hilbert correspond à un séquent naturel où il n'y a pas d'hypothèse.

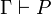
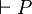
On peut montrer que ces trois systèmes sont équivalents dans le sens où ils ont exactement les mêmes théorèmes.

L'aspect « classique » du calcul des propositions est obtenu, dans le système à la Hilbert, par l'axiome de contraposition , il apparaît dans la déduction naturelle à travers la réduction à l'absurde. Le calcul des séquents est classique, mais si l'on se restreint aux séquents avec un seul conséquent, il devient intuitionniste.

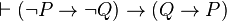
Sémantique

    Ce que j'ai appris de la logique, c'est cette dissociation entre vérité et prouvabilité. Alain Connes, in Triangle de pensées Ed. Odile Jacob, (2000).

La sémantique détermine les règles d'interprétations des propositions. Attribuer des valeurs de vérité à chacune des propositions élémentaires intervenant dans une proposition revient à choisir un modèle de cette proposition.

De façon plus précise, l'interprétation d'une proposition A est le fait d'attribuer une valeur de vérité (0 ou 1) aux variables propositionnelles et à expliquer comment les connecteurs se comportent vis-à-vis des valeurs de vérité. On donne ce comportement par une table de vérité. De cette manière on peut donner un valeur 0 ou 1 à chaque propositions qui dépend des valeurs prises par les tables de vérité. Il existe trois cas d'interprétation:

• Quand la proposition prend toujours la valeur 0 quelles que soient les valeurs des variables propositionnelles, la proposition est dite être une antilogie ou une contradiction. On dit également qu'elle est insatisfaisable.
• Lorsque la proposition A prend toujours la valeur 1, A est une tautologie. On dit aussi que A est valide et on notera cette assertion .
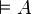
• Si la proposition prend au moins une fois la valeur 1, on dit que l'on peut satisfaire A, ou que A est satisfaisable (ou encore "satisfiable" par mimétisme avec le terme anglais).
• Si la proposition prend au moins une fois la valeur 1 et au moins une fois la valeur 0, c'est une proposition synthétique ou contingente.

Interprétation des connecteurs

Nous explicitons le comportement, puis donnons la table de vérité associée

• prendra la valeur 1 si et seulement si au moins l'une des deux propositions P ou Q prend la valeur 1.

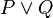
P	Q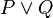
0	0	0
0	1	1
1	0	1
1	1	1

• prendra la valeur 1 si et seulement si les deux propositions P et Q prennent simultanément la valeur 1.

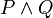
P	Q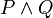
0	0	0
0	1	0
1	0	0
1	1	1

• prendra la valeur 0 si et seulement si P prend la valeur 1 et Q la valeur 0.

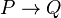
P	Q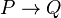
0	0	1
0	1	1
1	0	0
1	1	1

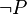
• p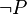rendra la valeur 1 si et seulement si P prend la valeur 0.

P
0	1
1	0

• prendra la valeur 1 si et seulement si P et Q ont la même valeur.

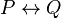
P	Q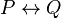
0	0	1
0	1	0
1	0	0
1	1	1

• prend la valeur 0.

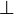
Exemple 1 :

(¬A → A) → A est une tautologie.

En effet, si on attribue à A la valeur 0, alors ¬A prend la valeur 1, (¬A → A) prend la valeur 0, et (¬A → A) → A prend la valeur 1. De même, si on attribue à A la valeur 1, alors ¬A prend la valeur 0, (¬A → A) prend la valeur 1, et (¬A → A) → A prend la valeur 1.

Exemple 2 :

A → (A → ¬A) n'est pas une tautologie.

En effet, si on attribue à A la valeur 1, alors ¬A prend la valeur 0, (A → ¬A) prend la valeur 0, et A → (A → ¬A) prend la valeur 0.

Systèmes complets de connecteurs

Une table de vérité à n entrées définit un connecteur n-aire. Un ensemble de connecteurs propositionnels est dit complet si tout connecteur peut se définir au moyen des connecteurs de l'ensemble. Toute table de vérité se décrit à l'aide de conjonctions de disjonctions et de négation, par exemple on décrit entièrement la table de vérité de l'équivalence ci-dessus par « p ↔ q prend la valeur vrai si et seulement si p et q prennent la valeur faux ou p et q prennent la valeur vraie », c'et-à-dire que p ↔ q ≡ (¬p ∧ ¬q) ∨ (p ∧ q). Cette méthode est générale et permet de montrer que le système {¬, ∧, ∨} est un système complet de connecteurs. On en déduit que {¬, ∧}, {¬, ∨} sont aussi des systèmes complets (à cause des lois de de Morgan, A∨B ≡ ¬ (¬A ∧ ¬B), A ∧ B ≡ ¬ (¬A ∨ ¬B)). L'ensemble {¬, →} est également complet : A ∨ B ≡ ¬A → B.

L'ensemble constitué du seul connecteur NON-ET (noté « | » par Henry Sheffer) est également complet, ¬P étant équivalent à P|P et P∨Q à (P|P) | (Q|Q). Cette particularité est utilisée pour la construction de circuits logiques, une seule porte suffisant alors pour concevoir tous les circuits existants.