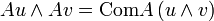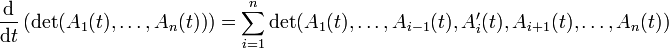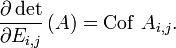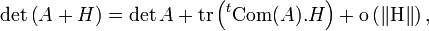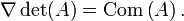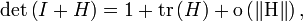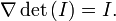Comatrice - Définition
La liste des auteurs de cet article est disponible ici.
Variations de la fonction déterminant
La formule de Leibniz montre que le déterminant d'une matrice A s'exprime comme somme et produit de composantes de A. Il n'est donc pas étonnant que le déterminant ait de bonnes propriétés de régularité. On suppose ici que K est le corps des réels.
Déterminant dépendant d'un paramètre
Si
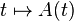

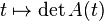

La formule de dérivation s'obtient en faisant intervenir les colonnes de A
Cette formule est analogue formellement à la dérivée d'un produit de n fonctions numériques.
Le déterminant comme fonction sur l’espace des matrices
- L’application qui à la matrice
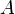
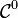
- Cette propriété a des conséquences topologiques intéressantes :
- ainsi le groupe
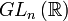
- le sous-groupe
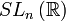
- Cette application est en fait différentiable (membre de
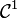
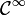
- En effet le calcul des cofacteurs peut être vu précisément comme un calcul de dérivée partielle
-
- Toutes ces dérivées partielles étant elles-mêmes des déterminants, par récurrence le déterminant est
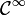
- En effet le calcul des cofacteurs peut être vu précisément comme un calcul de dérivée partielle
- En outre on peut écrire le développement limité à l’ordre un du déterminant au voisinage de
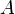
-
-
- c’est-à-dire que si on munit
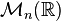
-
- Notamment pour le cas où
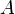
-
-
Propriétés de la comatrice
Nous avons
- com(In) = In
et
- pour toutes matrices M et N d'ordre n, com(MN) = com(N) com(M)
La comatrice est aussi compatible avec la transposition :
- com(tM) = t (com(M)).
de plus,
- det(com(M)) = det(M)n-1.
Si p(t) = det(M - tIn) est le polynôme caractéristique de M et que q est le polynôme défini par q(t) = (p(0) - p(t))/t, alors
- tcom(M) = q(M).
La comatrice apparaît dans la formule de la dérivée d'un déterminant.
Pour
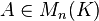
- si A est de rang n (i.e. A inversible), Com(A) aussi. On a alors
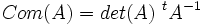
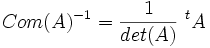
- si A est de rang n-1, Com(A) est de rang 1.
- si A est de rang au plus n-2, Com(A)=0.
Si
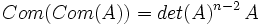
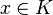
Si
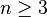
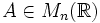
Comatrice et produit vectoriel
Si A est une matrice d'ordre trois, elle agit sur les vecteurs de l'espace à trois dimensions muni d'une base orthonormée d'orientation directe. La comatrice de A décrit alors l'interaction de A avec le produit vectoriel:
-