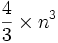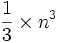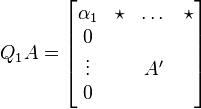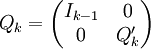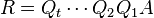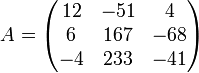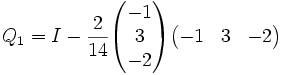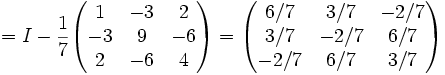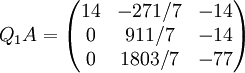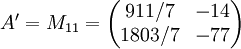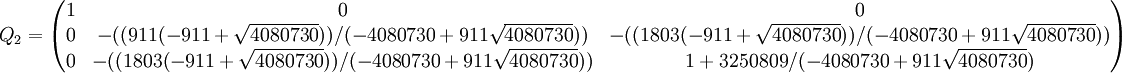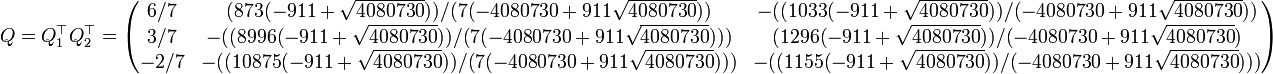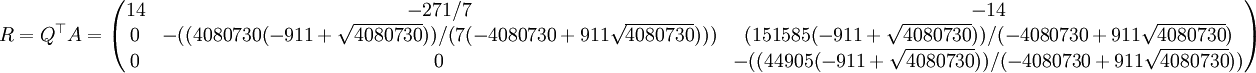Décomposition QR - Définition

Introduction

En algèbre linéaire, la décomposition QR (appelée aussi, décomposition QU) d'une matrice A est une décomposition de la forme

A = QR

où Q est une matrice orthogonale (QQ^T = I), et R une matrice triangulaire supérieure.

Il existe plusieurs méthodes pour réaliser cette décomposition :

• la méthode de Householder où Q est obtenue par produits successifs de matrices orthogonales élémentaires
• la méthode de Givens où Q est obtenue par produits successifs de matrices de rotation plane
• la méthode de Schmidt

Chacune d'entre elles a ses avantages et ses inconvénients. (La décomposition QR n'étant pas unique, les différentes méthodes produiront des résultats différents).

Méthode de Householder

Soit x un vecteur colonne arbitraire de dimension m et de longueur |α| (Pour des raisons de stabilité du calcul, α doit être du signe du premier élément de x et la longueur étant la somme de tous les éléments de x). Toutefois, plusieurs versions semblent exister à propos de α, ici, vous est présenté la version de l'article anglais. D'autres utilisent la norme || ||₂ plutôt que la longueur.

Soit e₁ le vecteur (1,0,..., 0)^T, et || || la norme euclidienne, définissons

.

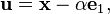
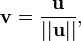
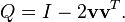
Q est la matrice de Householder ou matrice orthogonale élémentaire et

.

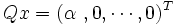
Nous pouvons utiliser ces propriétés pour transformer une matrice A de dimension m*n en une matrice triangulaire supérieure. Tout d'abord, on multiplie A par la matrice de Householder Q₁ en ayant pris le soin de choisir pour x la première colonne de A . Le résultat est une matrice QA avec des zéros dans la première colonne excepté du premier élément qui vaudra α.

Ceci doit être réitéré pour A' qui va être multiplié par Q’₂ (Q’₂ est plus petite que Q₁). Si toutefois, vous souhaiteriez utiliser Q₁A plutôt que A’, vous deviez remplir la matrice de Householder avec des 1 dans le coin supérieur gauche :

Après t itérations, t = min(m − 1,n),

est une matrice triangulaire supérieure. Si alors A = QR est la décomposition QR de A.

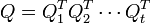
Calculons la décomposition QR de

On choisit donc le vecteur (cet exemple contient beaucoup d'erreurs alors faites attention) a₁ = (12,6, − 4)^T. On a donc . Ce qui nous conduit à écrire .

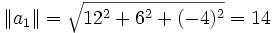
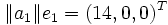
Le calcul nous amène à u = ( − 2,6, − 4)^T et . La première matrice de Householder vaut

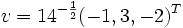
Observons que:

Nous avons maintenant sous la diagonale uniquement des zéros dans la 1^re colonne.

Pour réitérer le processus, on prend la sous matrice principale

Par la même méthode, on obtient la 2^e matrice de Householder

Finalement, on obtient

La matrice Q est orthogonale et R est triangulaire supérieure, par conséquent, on obtient la décomposition A = QR.

Coût et avantages

Le coût de cette méthode pour une matrice n*n est en : Ce coût est relativement élevé (la méthode de Cholesky, pour les matrices symétriques définies positives est en ). Cependant, la méthode de Householder présente l'avantage considérable d'être beaucoup plus stable numériquement, en limitant les divisions par des nombres petits. La méthode de Givens, malgré un coût encore supérieur à celui-ci, offrira encore davantage de stabilité.