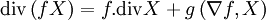Dérivée de Lie - Définition
La liste des auteurs de cet article est disponible ici.
Approche axiomatique générale
Il existe une unique application linéaire
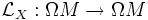
-
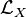
-
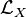
-
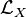
Définition dynamique
Soit φt le flot de X (pour t petit). On défini la dérivée de Lie d'un champ de tenseurs K par :
où
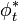
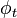
Formule de Cartan
Application :
Naturalité
Définition de la divergence
Dans Rn on a la formule suivante :
qu'on peut généraliser en définition de la divergence d'un champ de vecteur sur toute variété munie d'une forme volume ω, en particulier les variétés riemanniennes :
- .
Cette définition a bien un sens car en tout point x de M l'espace des formes multilinéaires alternée en degré maximal est de dimension 1.
Vu la définition dynamique donnée plus haut, le flot local du champ X préserve la forme volume si et seulement si sa divergence est nulle.
Pour la forme volume associée à une métrique riemannienne g on a :
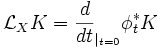
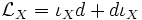
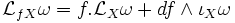
![\varphi^*\left[\mathcal{L}_X\omega\right]=\mathcal{L}_{\varphi^*X}\left[\varphi^*\omega\right]](https://static.techno-science.net/illustration/Definitions/autres/7/7f8c5af6d8447539c0a35f6a162dc829_db753ac8a026aa09b19c2467c7d10f20.png)
![\mathcal{L}_X\left[dx_1\wedge\dots\wedge dx_n\right]=\left[ \mathrm{div} X\right].dx_1\wedge\dots \wedge dx_n](https://static.techno-science.net/illustration/Definitions/autres/b/b2063634a1fc9af8b5e462344eef357c_1aa84168f828be9b013061814a7edca0.png)