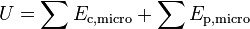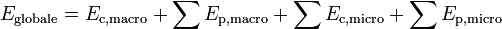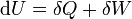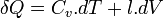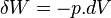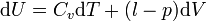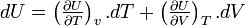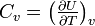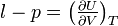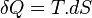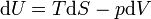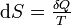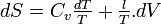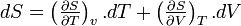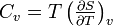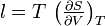Énergie interne - Définition

Introduction

Potentiels thermodynamiques
Énergie interne	U(S,V,N)
Énergie libre	F(T,V,N) = U − TS
Enthalpie	H(S,p,N) = U + pV
Enthalpie libre	G(T,p,N) = U + pV − TS

Un système thermodynamique est un objet constitué de molécules ou d’atomes qui possède une énergie totale pouvant être décomposée en deux parties:

1. une énergie cinétique correspondant au mouvement de l’objet dans son ensemble ainsi qu’aux mouvements des particules qui le constituent,
2. une énergie potentielle due aux interactions de l’objet avec le milieu extérieur par l’intermédiaire de champs, gravitationnel, électriques ou magnétiques mais aussi due aux interactions entre les molécules, ions, atomes, électrons, noyaux, nucléons… qui constituent ce système.

Il existe donc deux niveaux de réalité pour l’énergie totale du système :

1. Un niveau macroscopique, sensible à nos sens c’est-à-dire à notre échelle humaine, correspondant à l’énergie cinétique macroscopique du système en mouvement dans un référentiel donné : et aux énergies potentielles macroscopiques du système placé dans des champs de gravitation, électriques ou magnétiques : .
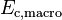
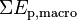
2. Un niveau microscopique inaccessible à nos sens, correspondant aux énergies cinétiques microscopiques que l’on peut assimiler à l’agitation thermique des particules : et à toutes les énergies potentielles d’interactions microscopiques que l’on peut assimiler, entre autres, aux énergies de liaison chimique et aux énergies d’interactions entre les nucléons (énergies nucléaires) : .

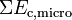
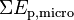
L’énergie interne U d'un système thermodynamique correspond à la somme de ses énergies microscopiques.

Énergie globale et énergie interne d'un système

L’énergie globale d'un système peut s’écrire :

Énergie interne

Par définition, la somme des énergies microscopiques constitue l’énergie interne U du système, c’est-à-dire son énergie propre :

Étant donné la complexité des interactions au niveau microscopique, l’énergie interne U n’est pas calculable et c’est ce qui explique que la plupart des fonctions d’état du système, qui en dépendent (exceptée l’entropie S), ne sont pas connues de façon absolue. On peut uniquement calculer leur variation. L’énergie interne est une fonction d'état du système. Sa variation ne dépend que de l’état final et de l’état initial d’équilibres et non pas de la nature de la transformation. Sa différentielle dU est une différentielle totale exacte.

Formes différentielles de l'énergie interne et coefficients calorimétriques

• D'après le premier principe de la thermodynamique

or

Dans le cas où seules des forces de pression sont en jeu :

donc

• Coefficients calorimétriques

L'énergie interne est une fonction d'état et sa différentielle est totale exacte.

Donc

• D'après le second principe de la thermodynamique

d'où

• Coefficients calorimétriques

Or l'entropie est une fonction d'état et sa différentielle totale est exacte.

Il s'ensuit que