Énergie libre - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Potentiels thermodynamiques | |
|---|---|
| Énergie interne | U(S,V,N) |
| Énergie libre | F(T,V,N) = U − TS |
| Enthalpie | H(S,p,N) = U + pV |
| Enthalpie libre | G(T,p,N) = U + pV − TS |
L'énergie libre F (appelée aussi "'énergie libre de Helmholtz"') est, en thermodynamique, une fonction d'état extensive dont la variation permet d'obtenir le travail utile susceptible d'être fourni par un système thermodynamique fermé, à température constante. Elle correspond à l'énergie libre de Helmholtz des anglo-saxons, qui préfèrent la symboliser par la lettre A.
Cette fonction ne doit pas être confondue avec la fonction enthalpie libre G ("énergie libre de Gibbs" des anglo-saxons), qui s'applique aux systèmes évoluant à la température T et à pression constante (cas des réactions effectuées à l'air libre).
L'énergie libre est souvent utilisée dans l'étude des explosions qui induisent une variation de pression ou encore dans la calorimétrie à volume constant effectuée dans une bombe calorimétrique.
Néanmoins le rôle de la fonction F est beaucoup moins important en thermochimie que celui de la fonction enthalpie libre qui est la fonction phare, indispensable à l’étude des équilibres chimiques.
Cette fonction, qui n'est en fait rien d' autre que le logarithme de la fonction de partition, joue un rôle fondamental en physique théorique. Pour finir, elle présente bien souvent des propriétés d'automoyennage qui justifient que ce soit à elle qu'on s'intéresse dans l'étude des systèmes désordonnés.
Définition
Considérons une transformation irréversible effectuée à la température T et à volume constant. S’il n’y a pas de montage électrochimique, il n’y a pas de travail électrique. Comme V=cte, le travail des forces de pression est nul.
Donc en appliquant le premier principe :
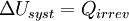
Appliquons alors le second principe : 
Le système échange avec le milieu extérieur Qirrév. Si on se place du côté du milieu extérieur, celui-ci reçoit - Q(irrév) = - ΔU(syst).
Et la variation d’entropie du milieu extérieur devient égale à :
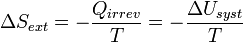
D’où : 
Multiplions par ( - T )
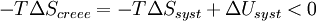
On définit ainsi la fonction énergie libre :
|
|
Pour une transformation effectuée à T et V = cte, on obtient :
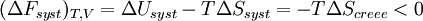
Si la transformation est réversible,
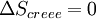
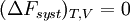
En revanche, si la transformation est irréversible,  et donc
et donc
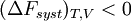
| La transformation réelle à T et V = cte, ne peut s’effectuer qu’avec une diminution de l’énergie libre du système. |
Relations utiles à partir de F ou de ses différentielles
- Relation de maxwell :
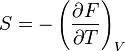
- Relation de Gibbs-Helmholtz : il existe une relation analogue à celle de Gibbs-Helmholtz concernant F :
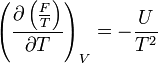
- Potentiel chimique : une "définition" du potentiel chimique peut être donnée à partir d'une différentielle partielle de F.
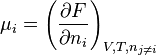
Différentielle de F
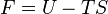
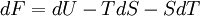
- Appliquons le premier principe
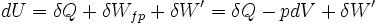
avec:
δWfp : travail des forces de pression
δW': travail autre, comme par exemple le travail électrique dans un montage de pile
- Appliquons le second principe
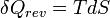
dU s'exprime donc:
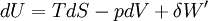
d'où :
|
|
- Si la température est constante:
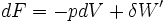
- Cas d'une transformation réelle donc irréversible
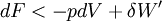
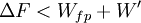
On montre bien que la variation de la fonction F est égale au travail fourni par le système si la transformation est réversible et est effectuée à T constante .
- Si le volume est constant et le travail W' est nul:
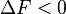
plus précisément :
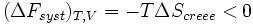
La transformation réelle à T et V = cte, ne peut s’effectuer qu’avec une diminution de l’énergie libre du système. On peut donc identifier F au potentiel thermodynamique d'une transformation isotherme et isochore