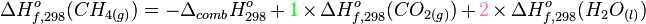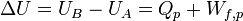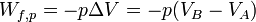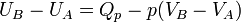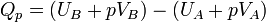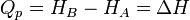Enthalpie - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Potentiels thermodynamiques | |
|---|---|
| Énergie interne | U(S,V,N) |
| Énergie libre | F(T,V,N) = U − TS |
| Enthalpie | H(S,p,N) = U + pV |
| Enthalpie libre | G(T,p,N) = U + pV − TS |
L'enthalpie (du préfixe en- et du grec thalpein : « chauffer ») est une fonction d'état extensive de la thermodynamique, dont la variation permet d'exprimer la quantité de chaleur mise en jeu pendant la transformation à pression constante (isobare) d'un système thermodynamique au cours de laquelle celui-ci reçoit ou fournit un travail mécanique.
Définition
Considérons une transformation isobare au cours de laquelle le système passe d’un état A à un état B d’équilibres en échangeant de la chaleur
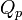
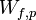
Le premier principe permet d’écrire :
U étant la fonction d'état énergie interne
À pression constante le travail des forces de pression est égal à :
Donc
D'où :
On définit ainsi une nouvelle fonction d’état, la fonction enthalpie
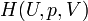
Il s'ensuit que :
Par conséquent, à pression constante, la chaleur mise en jeu, qui n’est pas une fonction d’état puisque c'est un transfert d'énergie entre le système et le milieu extérieur, devient égale à la variation de la fonction d’état enthalpie H. La variation de cette fonction ne dépend que de l’état final et de l’état initial du système et est indépendante du chemin suivi par la transformation.
C’est tout l’intérêt de l’application de la fonction enthalpie dans les cas très courants de transformations effectuées à l’air libre, à pression atmosphérique constante.
Cette propriété est à la base de la calorimétrie à pression constante. Par abus de langage on confond souvent les termes chaleur et enthalpie.
Différentielle de l'enthalpie
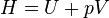
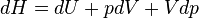
- Appliquons le premier principe
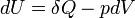
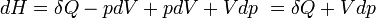
- Appliquons le second principe
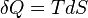
d'où
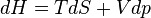
Propriétés
L'enthalpie a la dimension d'une énergie, et s'exprime en joules dans le Système International.
La propriété mathématique induite pour toute fonction d'état implique que sa différentielle est totale exacte c'est-à-dire qu'elle est égale à la somme des différentielles partielles par rapport à chaque variable.
État standard
État standard (conditions standards) : état de référence pour réactifs et produits : corps pur à p0= 1 bar ; T = cte ; C0 = 1 mol.L-1 pour un soluté.
État standard de référence : état physique le plus stable à p0 = 1 bar et T = cte.
Applications
- Application de l'enthalpie aux réactions chimiques effectuées à T et p constantes
Dans le cas d'une réaction chimique effectuée à T et p constantes, il a été défini une grandeur de réaction appelée enthalpie de réaction, associée à l'équation bilan de la réaction:
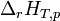
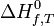
Exemple
L'exemple ci-dessous est celui d'une relation entre enthalpie standard de formation et enthalpie de réaction dans le cas de la combustion d'un alcane
Calcul de l'enthalpie de combustion du méthane à 298K sous la pression standard :
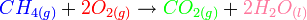
La loi de Hess permet d'écrire :
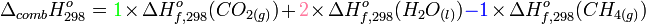
L'enthalpie standard de formation du dioxygène est nulle car c'est un corps pur simple stable dans les conditions choisies (voir enthalpie standard de formation).
Le calcul de cette enthalpie de combustion permet la détermination de la chaleur de réaction (voir enthalpie de réaction). Inversement, si l'on mesure cette chaleur à l'aide d'une bombe calorimétrique, on peut avoir accès à l'enthalpie standard de formation du méthane.