Potentiel thermodynamique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Potentiels thermodynamiques | |
|---|---|
| Énergie interne | U(S,V,N) |
| Énergie libre | F(T,V,N) = U − TS |
| Enthalpie | H(S,p,N) = U + pV |
| Enthalpie libre | G(T,p,N) = U + pV − TS |
Pour un système thermodynamique donné, un potentiel thermodynamique est une fonction particulière qui atteint un minimum à l'équilibre thermodynamique du système, et à partir de laquelle on peut déduire toutes les propriétés du système à l'équilibre. Différents potentiels thermodynamiques correspondent aux différents jeux de variables d'état utilisés.
Les quatre potentiels thermodynamiques les plus couramment utilisés sont :
| Nom | Formule | Variables naturelles |
| Énergie interne |
|
|
| Énergie libre de Helmholtz |
|
|
| Enthalpie |
|
|
| Enthalpie libre de Gibbs |
|
|
où T = température, S = entropie, P = pression, V = volume. L'énergie libre de Helmholtz est souvent notée F, mais l'utilisation de A est conseillée par l'Union internationale de chimie pure et appliquée. Ni est le nombre de particules de type i dans le système. On a inclus ici l'ensemble des Ni parmi les variables naturelles des potentiels thermodynamiques, mais il est souvent ignoré.
Description et interprétation
Les potentiels thermodynamiques sont très utiles pour calculer le résultat d'équilibre d'une réaction chimique ou bien pour mesurer les propriétés des espèces lors d'une réaction chimique. Les réactions chimiques ont en général lieu sous certaines contraintes simples comme à pression et température constantes, ou bien à entropie et volume constants; dans ce cas-là, on peut faire intervenir les potentiels thermodynamiques correspondants. Comme en mécanique, le système verra la valeur du potentiel diminuer, et à l'équilibre, sous ces contraintes, le potentiel va adopter une valeur minimale permanente. Les potentiels thermodynamiques peuvent également être utilisés pour estimer la quantité totale d'énergie disponible pour un certain système thermodynamique sous certaines contraintes.
En particulier (voir le principe de l'énergie minimale pour la dérivation) :
- Quand l'entropie (S) et les paramètres extensifs (par exemple le volume) d'un système fermé sont maintenus constants, l'énergie interne (U) diminue et atteint un minimum à l'équilibre. C'est une conséquence du premier et du deuxième principe de la thermodynamique, appelée principe de l'énergie minimale. Les trois énoncés ci-dessous sont directement déductibles de ce principe.
- Quand la température (T) et les paramètres extensifs d'un système fermé sont maintenus constants, l'énergie libre de Helmholtz (F) diminue et atteint un minimum à l'équilibre.
- Quand la pression (P) et les paramètres extensifs d'un système fermé sont maintenus constants, l'enthalpie (H) diminue et atteint un minimum à l'équilibre.
- Quand la température (T), la pression (P) et les paramètres extensifs d'un système fermé sont maintenus constants, l'enthalpie libre de Gibbs (G) diminue et atteint un minimum à l'équilibre.
Variables naturelles
Les variables maintenues constantes sont appelées variables naturelles de ce potentiel. Les variables naturelles sont importantes dans le raisonnement ci-dessus, mais également pour la raison suivante : si un potentiel thermodynamique peut être déterminé comme fonction de ses variables naturelles, toutes les propriétés thermodynamiques du système peuvent être déterminées en prenant les dérivées partielles de ce potentiel par rapport à ces variables naturelles (et ce n'est vrai pour aucune autre combinaison de variables). Réciproquement, si un potentiel thermodynamique n'est pas donné comme une fonction de ses variables naturelles, il ne pourra en général pas décrire toutes les propriétés thermodynamiques du système.
Variables conjuguées
Une petite augmentation d'énergie dans un système mécanique est le résultat d'une force multipliée par un petit déplacement. Ainsi une augmentation de l'énergie d'un système thermodynamique peut être exprimé comme une somme de produits de certaines "forces" généralisées, qui hors équilibre provoquent des "déplacements" généralisés. Le produit de cette "force" par ce "déplacement" représente l'énergie transférée. Ces forces et leurs déplacement associés sont appelés variables conjuguées.
Par exemple, considérons la paire conjuguée PV. La pression P agit comme une force généralisée : une différence de pression force un changement dans le volume dV, et leur produit est l'énergie perdue par travail par le système. Ici la pression est la force et le volume associé le déplacement, et les deux variables forment une paire de variables conjuguées. De même, les différences de température induisent des variations de l'entropie, et leur produit est l'énergie transférée par transfert de chaleur.
La force thermodynamique est toujours une variable intensive, et le déplacement une variable extensive. La variable intensive est la dérivée de l'énergie interne selon la variable extensive, avec toutes les autres variables extensives maintenues constantes.
D'autres variables conjuguées - le potentiel chimique
La théorie des potentiels thermodynamiques n'est pas complète tant que l'on ne considère pas le nombre de particules d'un système comme une variable à part entière comme les autres grandeurs extensives telles que le volume ou l'entropie.
Le nombre de particules est la variables de déplacement d'une paire de variables conjuguées. La force généralisée de cette paire est le potentiel chimique. Le potentiel chimique peut être vu comme une force qui, hors équilibre, induit des échanges de particules, soit avec l'extérieur, soit entre les phases d'un système. C'est un concept utile dans les cas de mélanges d'espèces et de phases.
Par exemple, pour un certain volume contenant de l'eau liquide et de la vapeur d'eau, il existe un potentiel chimique (négatif) pour le liquide qui pousse les molécules d'eau vers la vapeur (évaporation), et un potentiel chimique pour la vapeur, qui pousse les molécules de vapeur dans l'eau (condensation). Ce n'est que quand ces "forces" s'équilibrent et que les potentiels chimiques de chaque phase sont égaux que l'équilibre est atteint.
D'autres potentiels thermodynamiques
L'ensemble de variables naturelles pour les quatre potentiels thermodynamiques décrits ci-dessus sont formés de toutes les combinaisons de T-S et P-V, tant que l'on n'utilise pas deux variables conjuguées pour un même potentiel. Il n'y a pas de raison d'ignorer la paire conjuguée µi-Ni, et l'on peut donc définir quatre potentiels thermodynamiques additionnels pour chaque espèce. En utilisant les notations de l'UICPA, pour lesquelles les crochets contiennent les variables naturelles autres que les quatre principales, on obtient :
| Formule | Variables naturelles |
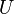
![U[\mu_j]=U-\mu_jN_j\,](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/269912f4aa53f453130defff4762ac97_16cff82133307ee01330d03408db9e0f.png)
|
|
![A[\mu_j]=U-TS-\mu_jN_j\,](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/fbf99160142ff7ad27d5bc26816c2fdb_91d3715e13aca25b298b5d828cadae13.png)
|
|
![H[\mu_j]=U+PV-\mu_jN_j\,](https://static.techno-science.net/illustrationWebp/Definitions/autres/5/5b1c9d3955948331e446f094dd0bf5e7_a8a26dbec26cbcc128834386511d5b67.png)
|
|
![G[\mu_j]=U+PV-TS-\mu_jN_j\,](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/447d4f512a5c09213e4f4bceea569229_1cecc05755de57f772ae8d1140b60575.png)
|
|
S'il y a par exemple deux espèces, il y aura des potentiels additionnels comme U[µ1,µ2] = U - µ1N1 - µ2N2 etc... S'il y a D dimensions dans l'espace thermodynamique, il y aura 2D potentiels thermodynamiques uniques. Pour le cas le plus simple, un gas idéal à phase unique, il y a trois dimensions, et donc huit potentiels thermodynamiques.
