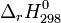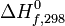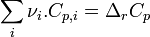Thermochimie - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La thermochimie est une partie de la chimie qui étudie les phénomènes thermiques qui accompagnent les réactions chimiques. Certaines réactions peuvent dégager de la chaleur, elles sont exothermiques et d’autres en absorbent, elles sont endothermiques. Marcellin Berthelot est considéré comme le fondateur de la thermochimie. Il créa la bombe calorimétrique et participa au perfectionnement du calorimètre. La bombe calorimétrique, qui est une très grande invention, permet de mesurer le pouvoir calorifique d’un combustible; la capacité d’un combustible à produire de l’énergie. Mise au point en 1881, elle est encore en usage aujourd’hui.
Au cours du XXe siècle, la thermochimie s’est beaucoup développée. L’application du second principe de la thermodynamique aux systèmes chimiques a permis de prévoir le sens des réactions, le positionnement des équilibres chimiques et donc de définir le rendement et la composition du système après réaction.
Définitions
Chaleur de réaction
Au cours d’une réaction chimique, le système échange de l’énergie avec le milieu extérieur sous forme de chaleur.
Cette énergie échangée sous forme de chaleur Q dépend des conditions expérimentales dans lesquelles se produit la réaction :
- À volume constant (transformation isochore), la thermodynamique montre que Q est égale à la variation d'énergie interne du système: Qv = ΔU (cas de la bombe calorimétrique).
- À pression constante, la chaleur est égale à la variation d’enthalpie: Qp = ΔH (cas très fréquent des réactions effectuées à l’air libre).
Enthalpie libre
L'enthalpie libre, G est la fonction d'état indispensable pour l'étude des équilibres chimiques. Elle permet en effet de définir si une réaction chimique effectuée à T et p constante, est thermodynamiquement possible et dans quel sens elle aura lieu. Si l'enthalpie libre de réaction est inférieur à 0 la réaction sera thermodynamiquement possible.
Opérateur de Lewis
On appelle opérateur de Lewis, noté
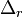
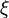
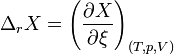
Enthalpie de réaction
On appelle enthalpie de réaction à T et p constantes, la grandeur
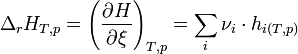
La variation d'enthalpie du système réactionnel, pour un état d'avancement donné, correspond à la chaleur mise en jeu et est égale à:
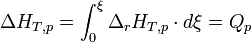
- Dans le cas d'un système idéal,
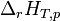
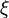
- On en déduit:
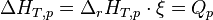
- On pourrait considérer que l'enthalpie de réaction
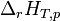
Si la réaction est effectuée de telle manière que chaque constituant se trouve sous la pression standard, p0, on obtient l'enthalpie standard de réaction,
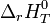
- pour un gaz : gaz parfait sous la pression de 1 bar,
- pour un liquide ou solide : sous la pression de 1 bar,
- pour un soluté : à une concentration de référence de
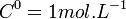
Une réaction chimique ne peut être étudiée thermodynamiquement, qu'à température et pression constante. Le plus souvent la pression choisie est la pression atmosphérique (1,01325 bar), assimilée à la pression standard. On obtient alors l'enthalpie standard de réaction à T.
Il est possible de calculer l'enthalpie standard de réaction à une température donnée connaissant l'enthalpie standard de réaction à 298K, température de référence des tables thermodynamiques.
L'évolution de l'enthalpie standard de réaction en fonction de la température est donnée par la loi de Kirchoff:
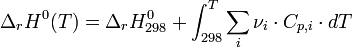
-
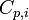
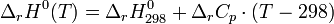
Attention : Cette relation n'est valable que s'il n'y a pas de changement d'état ou de phase dans l'intervalle de température considéré. Dans le cas contraire, il est nécessaire d'effectuer un cycle grâce à la loi de Hess pour les prendre en considération.
Le calcul de