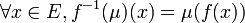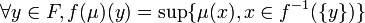Ensemble flou - Définition
La liste des auteurs de cet article est disponible ici.
Opérations
En observant comment les opérations usuelles se comportent vis-à-vis des fonctions caractéristiques de parties, on étend ces opérations aux fonctions d'appartenance des parties floues.
Réunion
Soient
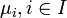
-
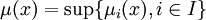
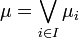
Intersection
De même, on définit l'intersection de ces parties au moyen de la fonction d'appartenance suivante :
-
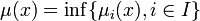
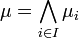
Réunion et intersection restent distributives l'une par rapport à l'autre.
Complémentaire
Le complémentaire d'une partie floue donnée par sa fonction d'appartenance μ est la partie floue dont la fonction d'appartenance est 1 − μ.
Le complémentaire d'une intersection reste égal à la réunion des complémentaires, et le complémentaire d'une réunion est l'intersection des complémentaires. Le complémentaire du complémentaire redonne la partie initiale.
Cependant, la réunion d'une partie floue et de son complémentaire ne donne pas toujours l'ensemble E, et l'intersection d'une partie floue et de son complémentaire ne donne pas l'ensemble vide.
En effet, considérons, par exemple, la partie floue F de E donnée par la fonction d'appartenance:
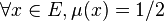
Cette partie floue est égale à son complémentaire car sa fonction d'appartenance vérifie μ = 1 − μ.
On déduit alors de
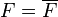
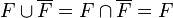
Image réciproque
Soient E et F deux ensembles et f une application de E dans F. Considérons une partie floue de F donnée par sa fonction d'appartenance μ. On appelle image réciproque de cette partie floue par f la partie floue de E donnée par la fonction d'appartenance suivante, notée f − 1(μ) :
Image directe
Soient E et F deux ensembles et f une application de E dans F. Considérons une partie floue de E donnée par sa fonction d'appartenance μ. On appelle image directe de cette partie floue par f la partie floue de F donnée par la fonction d'appartenance suivante, notée f(μ) :