Ensemble flou - Définition

Topologie floue

Dès 1968, Chang a appliqué la théorie des ensembles flous à la topologie, donnant naissance à la topologie floue.

Définition

Soit E un ensemble. Une topologie floue est donnée par une collection δ de fonctions d'appartenance vérifiant les propriétés suivantes :

(i) les fonctions 0 et 1 appartiennent à la collection δ

(ii) La borne inférieure d'un nombre fini d'éléments de δ est élément de δ

(iii) La borne supérieure d'un nombre quelconque d'éléments de δ est élément de δ.

Les éléments de δ sont les ouverts flous. Leurs complémentaires sont les fermés flous. La propriété (i) exprime que l'ensemble E et l'ensemble vide sont des ouverts flous, la propriété (ii) qu'une intersection finie d'ouverts flous est un ouvert flou et la propriété (iii) qu'une réunion quelconque d'ouverts flous est un ouvert flou.

Par exemple, étant donné un espace E muni d'une topologie τ au sens usuel, on peut lui associer une topologie floue naturelle ω(τ) en prenant pour δ la collection des fonctions semi-continues inférieurement à valeurs dans [0,1]. La topologie floue ainsi définie est dite engendrée par la topologie initiale τ de E. Réciproquement, si δ est une topologie floue définie sur E, on peut lui associer une topologie ι(δ) au sens usuel, à savoir la topologie la moins fine rendant toutes les fonctions de δ semi-continues inférieurement.

Notions topologiques

On peut alors introduire des notions plus complexes de topologie floue.

Continuité

Ainsi une fonction est continue floue si et seulement si l'image réciproque d'un ouvert flou de l'ensemble d'arrivée est un ouvert flou de l'ensemble de départ. Les fonctions constantes sont continues floues si et seulement si la topologie floue de l'espace de départ contient tous les ouverts flous définis par des fonctions d'appartenance constantes.

Compacité

Par analogie à la notion topologique usuelle, un espace topologique flou est compact si, de tout recouvrement par des ouverts flous, on peut extraire un recouvrement fini. Si l'image d'un compact par une application continue floue est compacte, en revanche, le théorème de Tychonov n'admet qu'une version limitée : seul le produit fini de compacts en topologie floue est compact. Plus généralement, soit L un treillis complet, distributif et complémenté d'élément maximum 1, soit α un nombre cardinal et soit une famille de compacts en topologie L-floue, où I est de cardinal α. Alors le produit des X_i est compact pour la topologie produit L-floue si et seulement si 1 vérifie la propriété suivante : pour toute famille d'éléments de L strictement inférieurs à 1, est strictement inférieur à 1 (théorème de Tychonov pour la topologie L-floue). Dans le cas où L = {0,1}, donnant la topologie usuelle, cette propriété est vérifiée pour tout cardinal α et un produit quelconque de compacts est compact. Mais si L = [0,1], donnant la topologie floue, la propriété n'est vérifiée que pour les cardinaux finis.

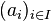
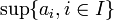
Lowen a proposé une autre définition des compacts en topologie floue. En effet, si la topologie floue comprend toutes les fonctions d'appartenance constantes, il n'existe pas de compact au sens précédent : les fonctions sont telles que donc ces fonctions définissent un recouvrement de l'espace mais il n'en existe pas de sous-recouvrement fini. Un espace E est compact pour la topologie floue au sens de Lowen si, pour toute fonction d'appartenance constante ν, tout ε > 0 et toute famille d'ouverts flous telle que , il existe une sous-famille finie telle que . Avec cette définition, un espace muni d'une topologie τ usuelle est compact si et seulement s'il est compact muni de la topologie floue ω(τ) engendrée par τ, et un produit quelconque d'espaces compacts est compact (théorème de Tychonov pour la topologie floue au sens de Lowen).

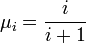
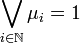
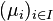
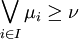
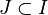
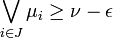
Enfin, on montre que le théorème de Tychonov pour la topologie L-floue et le théorème de Tychonov pour la topologie floue au sens de Lowen sont, comme le théorème de Tychonov usuel, équivalents à l'axiome du choix.