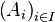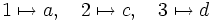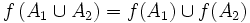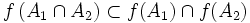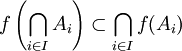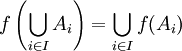Image directe - Définition
L'image directe d'un sous-ensemble A de X par une application 
est le sous-ensemble de Y formé des éléments qui ont au moins un antécédent par f d'un élément de A :
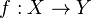
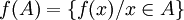
,- ou
.
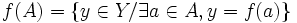
Si A=X, alors f(X) est appelée l'image de (l'application) f.
On se gardera bien de confondre l'image directe par f d'une partie de X, avec l'image par f d'un élément x de X.
Exemple : Considérons l'application 
, définie par
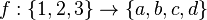
L'image directe de {2,3} par f est f({2,3})={c,d} tandis que l'image de f est {a,c,d}.
Propriétés élémentaires
- Pour toutes parties A1 et A2 de X,
L'inclusion dans l'autre sens est fausse en général. Considérons l'unique application 
. L'image par f de toute partie non vide est le singleton {0}.
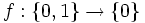
![\left[ \forall A_1 \subset X, \forall A_2 \subset X, f\left(A_1 \cap A_2\right) = f(A_1) \cap f(A_2)\right] \Leftrightarrow f\ {\rm injective}](https://static.techno-science.net/illustration/Definitions/autres/4/4a1eb2d08047f9fb5b34daf5464bc461_01257876324b67ea4bc64476f82c0eb2.png)
.
- pour toute partie B de Y,
.
.
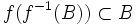
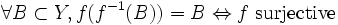
- pour toute partie A de X,
.
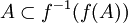
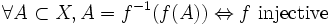
- Pour toute famille
de parties de X,
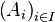
- Pour toute famille de parties de X,
Populaires