Ensemble flou - Définition

Introduction

La théorie des sous-ensembles flous est une théorie mathématique du domaine de l’algèbre abstraite. Elle a été développée par Lotfi Zadeh en 1965 afin de représenter mathématiquement l'imprécision relative à certaines classes d'objets et sert de fondement à la logique floue.

Présentation

Les sous-ensembles flous (ou parties floues) ont été introduits afin de modéliser la représentation humaine des connaissances, et ainsi améliorer les performances des systèmes de décision qui utilisent cette modélisation.

Les sous-ensembles flous sont utilisés soit pour modéliser l'incertitude et l'imprécision, soit pour représenter des informations précises sous forme lexicale assimilable par un système expert.

Propriétés

• Une partie floue A de E est caractérisée par une application de E dans [0,1]. Cette application, appelée fonction d'appartenance et notée μ_A représente le degré de validité de la proposition « x appartient à A » pour chacun des éléments x de E. Si μ_A(x) = 1, l'objet x appartient totalement à A, et si μ_A(x) = 0, il ne lui appartient pas du tout. Pour un élément x donné, la valeur de la fonction d'appartenance μ_A(x) est appelée degré d'appartenance de l'élément x au sous-ensemble A.

• L'ensemble E est donné par la fonction d'appartenance identiquement égale à 1. L'ensemble vide est donné par la fonction d'appartenance identiquement nulle.

• Le noyau d'une partie floue A est l'ensemble des éléments qui appartiennent totalement à A c'est-à-dire dont le degré d'appartenance à A vaut 1.

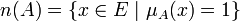
• Le support d'une partie floue A est l'ensemble des éléments appartenant, même très peu, à A c'est-à-dire dont le degré d'appartenance à A est différent de 0.

• La hauteur d'un sous-ensemble flou A de E est définie par .

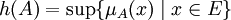
• Une partie floue A de E peut aussi être caractérisée par l'ensemble de ses α-coupes. Une α-coupe d'une partie floue A est le sous-ensemble net (classique) des éléments ayant un degré d'appartenance supérieur ou égal à α.

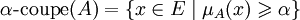
• Un ensemble fini possède un nombre fini de sous-ensembles L-flous si et seulement si le treillis L est fini. Si L = [0,1], un ensemble fini possède une infinité de sous-ensembles flous.

Définition

Ensemble flou. Le niveau de gris indique le degré d'appartenance.

Une partie A d'un ensemble E est usuellement associée à sa fonction caractéristique. Celle-ci s'applique sur les éléments x de E. Elle prend la valeur 0 si x n'appartient pas à A et 1 si x appartient à A.

On souhaite définir une partie A floue de E en attribuant aux éléments x de E un degré d'appartenance, d'autant plus élévé qu'on souhaite exprimer avec certitude le fait que x est élément de A. Cette valeur vaudra 0 si on souhaite exprimer que x de façon certaine n'est pas élément de A, elle vaudra 1 si on souhaite exprimer que x appartient à A de façon certaine, et elle prendra une valeur comprise entre 0 et 1 suivant qu'on estime plus ou moins certain l'appartenance de x à A. On est donc amené à définir une partie floue de la façon suivante :

Une partie floue (ou sous-ensemble flou) d'un ensemble E est une application de E dans [0,1].

Plus généralement, si L est un treillis complet, distributif et complémenté, on définit une partie L-floue comme étant une application de E dans L. Si L = [0,1], on retrouve la définition précédente de partie floue, et si L = {0,1}, on retrouve la notion usuelle de partie de E.