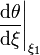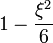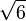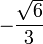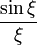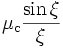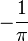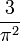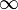Équation de Lane-Emden - Définition
La liste des auteurs de cet article est disponible ici.
Solutions de l'équation
Les conditions initiales de l'équation sont
- θ(0) = 1,
-
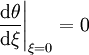
L'équation est définie tant que θ est positif. La solution pour une valeur de n donnée est en général notée θn. Le point où θ s'annule est en général noté ξ1.
Solutions exactes
Lorsque n vaut 0 ou 1, l'équation différentielle est homogène. Sa solution se trouve sans difficulté. Les autres valeurs de n sont significativement plus complexes, l'équation différentielle étant alors non linéaire. Un autre solution exacte existe cependant pour n = 5. Cette solution fut trouvée par Arthur Schuster en 1883, puis indépendamment par Emden plus tard. Les trois solutions analytiques connues s'écrivent :
| n | θ | μ | ξ1 |
|
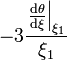
|
|---|---|---|---|---|---|
| 0 |
| μc |
|
| 1 |
| 1 |
|
| π |
|
|
| 5 |
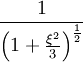
|
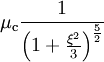
|
| 0 | 0 |
La solution est une sphère de densité constante lorsque n vaut 0 et elle se réduit à une équation différentielle sphérique de Bessel qui se résout en sinus cardinal lorsque n = 1.
Solutions singulières
Si l'on oublie les conditions initiales régulières de l'équation, un ensemble de solutions singulières (avec la densité divergeant au centre) peut aisément être trouvé sous la forme
-
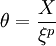
avec
-
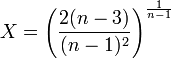
-
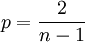
Ces solutions singulières n'existent que pour n plus grand que 3, c'est-à-dire γ inférieur à 4/3. Cette valeur critique apparaît dans de nombreux cas relatifs à cette équation.