Équation de Lane-Emden - Définition

Équations du problème de Lane-Emden

L'équation de Lane-Emden a pour but de décrire le profil de densité d'un fluide sans rotation soumis à l'action de son propre champ gravitationnel et possédant une équation d'état polytropique. L'état d'équilibre d'un fluide est appelé équilibre hydrostatique. Il est déterminé par l'équilibre entre le champ gravitationnel g du fluide et les forces de pression, selon la loi :

.

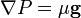
Le champ gravitationnel est relié au potentiel gravitationnel Φ par la relation :

,

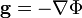
lui-même relié à la masse volumique par l'équation de Poisson :

ΔΦ = 4πGμ,

G étant la constante de gravitation. Enfin, le fluide étant un polytrope, pression et masse volumique sont reliées par la loi donnée ci-dessus ( ).

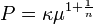
L'équation de Lane-Emden consiste en une réécriture de l'équation de Poisson utilisant dans un premier temps la relation entre le potentiel gravitationnel Φ et le champ g, puis entre g et la pression P, qui est enfin remplacée par sa valeur en termes de la masse volumique μ. Une fois ceci réalisé, un changement de variables est effectué, de façon à rendre l'équation plus maniable.

Masse et rayon

Rayon

Le rayon et la masse de la solution se déduisent assez rapidement de la solution une fois celle-ci connue. Par définition de ξ, le rayon physique de la configuration est donné par

.

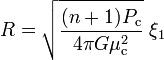
En remplaçant la pression centrale par sa valeur donnée par l'équation d'état, on obtient

.

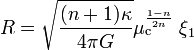
Ce résultat appelle plusieurs commentaires :

• Quand n est inférieur à 1, c'est-à-dire γ grand, le rayon est une fonction décroissante de la densité centrale.
• Quand à l'inverse n est supérieur à 1, le rayon est une fonction croissante de la densité centrale. Cela signifie qu'alors que la masse est de plus en plus concentrée en une région petite, l'extension totale de la configuration augmente de plus en plus, le gros du volume étant occupé par une matière de faible densité.
• Le cas où γ vaut 2 (c'est-à-dire n vaut 1) est particulier, car le rayon ne dépend pas de la densité centrale, sa valeur étant donnée par

.

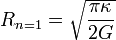
Masse

La masse quant-à elle se trouve en intégrant la relation

,

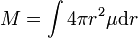
que l'on réécrit

.

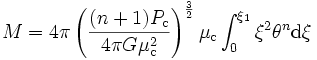
Or l'intégrand est une quantité qui apparaît explicitement dans la version compacte de l'équation de Lane-Emden. On en tire alors

.

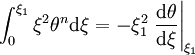
Il vient au final, en exprimant à nouveau la pression centrale en termes de l'équation d'état,

.

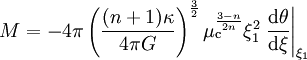
Cette fois, c'est la valeur n = 3 qui est singulière : la masse de la configuration ne dépend pas de la densité centrale : elle est indépendante de tout paramètre, et ne peut par conséquent prendre qu'une seule valeur. Ceci suggère fortement l'apparition d'une instabilité au moment ou le fluide atteint ce comportement (par un lent changement de l'indice n par exemple).

On peut ainsi exprimer le rayon en fonction de la masse. Abstraction faite d'un facteur numérique (dépendant de n), on a la relation

.

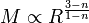
Ce résultat est intuitif pour la limite est grands γ (n nul). Le fluide est alors incompressible, sa densité est constante, et la masse est proportionnelle au cube du rayon.

Un autre écriture donne

.

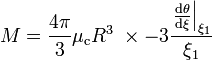
Le dernier facteur donne l'écart entre la masse approximée en supposant la densité centrale représentative de la densité moyenne, et la vraie masse. Dans le cas d'un fluide incompressible (n nul), ce dernier terme vaut 1 car la densité centrale est égale à la densité moyenne. À mesure que n croît, le facteur diminue, signe que la masse est concentrée dans une région petite par rapport à l'extension totale de la configuration.

Énergie de la configuration

La configuration possède une énergie potentielle de gravitation, ainsi qu'une énergie interne la formule donnant la première est appelée formule de Betti-Ritter, du nom de Enrico Betti et A. Ritter qui l'ont découverte.

Développements limité et asymptotique

L'équation de Lane-Emden ayant été découverte bien avant le développement des ordinateurs et autres moyens automatisés de calcul, et n'offrant pas (sauf cas particuliers évoqués ci-dessus) de solution exacte, elle a été l'objet de nombreuses études visant à proposer des approximations de ses solutions. Ainsi, des développements limités ont été proposés jusqu'à des ordres élevés en vue de tabuler les solutions. Au voisinage de 0, la solution peut ainsi être approximée selon :

.

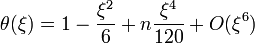
Pour les configurations s'étendant à l'infini, un développement asymptotique conduit immédiatement à

.