Équation de Lane-Emden - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En astrophysique, l'équation de Lane-Emden décrit la structure d'un objet dont l'équation d'état est celle d'un polytrope, et qui est soumis à l'influence de son propre champ gravitationnel. Il est de plus supposé que l'objet est à symétrie sphérique, c'est-à-dire qu'il n'est pas significativement déformé par sa propre rotation. L'équation de Lane-Emden permet alors de déterminer le profil de pression et de densité de l'objet, ainsi que de déterminer les type de configuration qu'il peut avoir (stable ou instable, d'extension finie ou infinie). Cette équation est nommée en l'honneur des astrophysiciens Jonathan Lane et Robert Emden. Y sont également liés Lord Kelvin et A. Ritter à la fin du XIXe siècle puis dans le courant des années 1930 Ralph H. Fowler et Subrahmanyan Chandrasekhar. Selon ce dernier, les travaux de Ritter sur ce problème sont plus importants que ceux d'Emden, et l'équation mériterait tout autant de s'appeler équation de Lane-Ritter.
C'est Jonathan Lane qui le premier proposa cette équation, en 1870, dans un travail qui est présenté comme étant le premier visant à étudier la structure interne d'une étoile.
Contexte scientifique
Un fluide polytropique, est un fluide dont la pression P est reliée à la masse volumique μ par l'équation d'état polytropique :
- P = κμγ,
où κ est une constante et γ un nombre appelé indice adiabatique. En pratique, on définit l'indice polytropique n par :
-
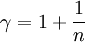
La raison du choix du terme d'indice polytropique plutôt que d'indice adiabatique tient à ce qu'en pratique, il peut y avoir des échanges de chaleur au sein du fluide considéré (par exemple du fait du flux d'énergie issu des réactions de fusion nucléaire au cœur d'une étoile).
Les fluides polytropiques jouent un rôle essentiel en astrophysique : de la matière dégénérée, c'est-à-dire dont la pression est déterminée par la pression de dégénérescence prédite par le principe d'exclusion de Pauli, se comporte comme un polytrope, dont l'indice polytropique varie selon que la matière est relativiste ou non relativiste (il vaut 3 et 3/2 respectivement). Le cœur de plusieurs types d'étoiles peut être considéré en très bonne approximation comme étant composé de matière dégénérée. Il en est de même pour les cadavres d'étoiles que sont les naines blanches et les étoiles à neutrons. De plus, dans une situation où la matière est en équilibre thermique, elle peut être vue comme un polytrope d'indice adiabatique égal à 1. Ce type de configuration est appelé, dans le contexte astronomique, sphère isotherme. En dehors du cadre de la description d'un nuage de gaz, il décrit aussi avec grande précision la structure des amas globulaires, qui en réalité peuvent être vus comme étant un « gaz » d'étoiles « isotherme », c'est-à-dire au sein duquel la vitesse de dispersion des étoiles est indépendante de la distance au centre de l'amas.
Formulation
L'équation de Lane-Emden peut s'écrire
-
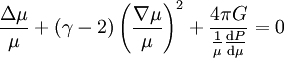
L'équation de l'équilibre hydrostatique peut se réécrire
-
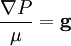
La pression étant une fonction de la masse volumique, le gradient de pression que s'écrire
-
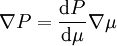
En substituant et en prenant la divergence, on obtient
-
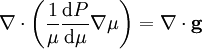
La divergence du champ g s'exprime en fonction du potentiel gravitationnel Φ, qui lui-même peut être remplacé par l'utilisation de l'équation de Poisson. On trouve au final
-
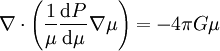
Le membre de gauche peut se réécrire
-
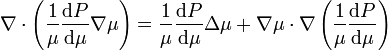
Au final, l'équation peut se réécrire
-
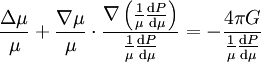
D'après l'équation d'état polytropique, la quantité
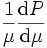
-
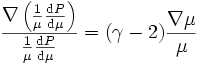
et finalement
-
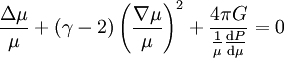
Dans le cas où l'exposant γ est différent de 1, c'est-à-dire que n est fini, cette équation peut se réécrire de façon plus compacte et élégante sous la forme
-
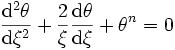
avec la quantité θ définie par
- μ = μcθn,
et ξ par
-
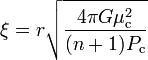
r étant la coordonnée radiale en coordonnées sphériques et l'indice c désignant les quantités évaluées au centre de la configuration.
En développant le terme faisant intervenir la pression et en se plaçant en coordonnées sphériques, et en notant par une prime les dérivées par rapport à la coordonnée radiale r, il vient
-
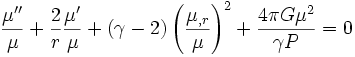
Il existe une formulation plus élégante de cette équation, obtenue en effectuant un changement de la variable μ. En considérant une quantité θ telle que
-
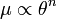
on obtient la simplification suivante :
-
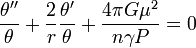
Si on note par un indice c les valeurs centrales de la densité et de la pression, et que l'on définit la normalisation de θ par
- μ = μcθn,
alors on obtient
-
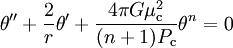
Enfin, on peut remarquer que la quantité
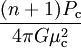
-
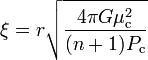
En notant par une prime les dérivées par rapport à ξ, il vient finalement
-
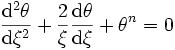
que l'on peut aussi écrire
-
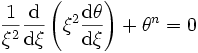
Le cas particulier où n est infini (γ = 1) est appelé sphère isotherme. Il possède de nombreuses caractéristiques atypiques et fait l'objet d'un article séparé.

















































