Équation polynomiale - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une équation polynomiale est une équation de la forme :
où les
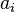
En mathématiques, l'équation polynomiale, est le sujet central de la théorie des équations. L'objectif de la théorie des équations est de trouver les racines d'un polynôme, ce qui revient à résoudre une équation polynomiale. Résoudre l’équation consiste à trouver l’ensemble des valeurs de l’inconnue
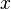
On appelle degré de l’équation la plus grande puissance de l’inconnue affectée d’un coefficient non nul. Par exemple, l’équation
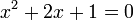
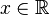
Théorie
Polynômes
Soit l’équation
dont les coefficients ai appartiennent à un corps


obtenu en substituant à l'inconnue x l'indéterminée X.
On montre en algèbre qu'un polynôme de degré n possède au plus n racines. L'équation (E) admet donc au plus n solutions.
Si
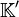

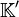

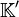

Existence de solutions pour les équations réelles et complexes
Le théorème de d'Alembert-Gauss affirme que le corps des complexes est algébriquement clos, c’est-à-dire que toute équation polynomiale à coefficients complexes et de degré au moins un admet une solution.
Il s’ensuit que toute équation polynomiale de degré un ou plus à coefficients réels admet une solution complexe. En revanche, une équation comme x2 + 1 = 0 n’a pas de solution dans

Autant l'intuition des solutions réelles d'équations réelles P(X) = 0 est immédiate (ce sont les points de la courbe Y=P(X) qui rencontrent l'axe (ox)), autant l'existence de ces solutions complexes d'équations réelles peut paraître étonnante et leur localisation indéterminable intuitivement.
Toutefois, une équation polynomiale réelle de degré impair admet nécessairement une solution réelle. En effet, la fonction polynôme associée est continue, et elle tend vers




Lien avec la théorie de Galois
On dispose de formules donnant les solutions des équations polynomiales réelles ou complexes de degré inférieur ou égal à 4 en fonction de leurs coefficients. Abel a montré qu’il n’est pas possible de trouver de telles formules générales (n’utilisant que les quatre opérations usuelles et les racines) pour les équations de degré 5 ou plus. La théorie de Galois donne un critère permettant de déterminer, étant donnée une équation polynomiale, si sa solution s’exprime par radicaux.
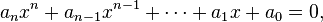
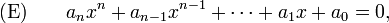
![P = a_n X^n + a_{n - 1} X^{n - 1} + \cdots + a_1 X + a_0 \quad \in \mathbb K[X],](https://static.techno-science.net/illustration/Definitions/autres/a/a6777d8338fc371c90e7aaa1d0e31fd6_f4c7295a0bf9c217e81f4db866276f9a.png)

















































