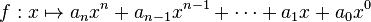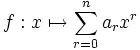Fonction polynôme - Définition

En algèbre, une fonction polynôme, ou fonction polynomiale est définie comme étant une application associée à un polynôme à coefficients dans un anneau (souvent un corps) commutatif K de la forme :

où n est un entier naturel et a_n, a_{n − 1}, ..., a₀ sont des éléments de K, appelés coefficients de la fonction polynôme f. Cela s'écrit encore, à l'aide de la notation sigma :

On dit que f est une fonction polynôme à coefficients dans K.

On n'a pas précisé les ensembles de départ K et d'arrivée L d'une fonction polynôme afin de ne pas compliquer la définition. Il suffit en fait que L soit muni d'une structure d'algèbre sur le corps (ou l'anneau) K. Une telle structure comporte toutes les opérations qui interviennent dans la définition d'une fonction polynôme :

• Les lois internes de multiplication et d'addition de l'anneau K permettent de multiplier et d'ajouter les coefficients entre eux.
• Une loi externe de multiplication permet de faire le produit d'un élément de l'anneau K et d'un élément d'un ensemble L.
• Une loi de multiplication interne permet de faire le produit de l'élément x avec lui-même dans l'ensemble L.
• Une loi d'addition interne permet d'ajouter entre eux les éléments de la forme a_kx^k appartenant à L.

Dans la pratique, on se place souvent dans les cas particuliers (ou ) dans lesquels toutes les lois de multiplications précédentes sont confondues.

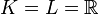
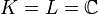
En analyse, on considère presque toujours des fonctions polynômes à coefficients réels ou complexes ( ou ).

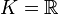
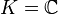
Degré

Le degré d'une fonction polynômiale f non nulle est le plus grand des entiers naturels k tels que a_k soit non nul (c'est donc n si le coefficient a_n n'est pas nul). Par convention, le degré de la fonction polynômiale nulle est .

Chaque terme de la fonction polynôme de la forme a_kx^k est appelé un monôme (de degré k). Le coefficient du monôme de plus haut degré est appelé le coefficient dominant de f ; a₀ est appelé le coefficient constant de f.

Identification des coefficients

Dans le cas où K est un corps commutatif infini, il y a équivalence entre l'identité formelle de polynômes à coefficients dans K et l'identité des fonctions polynômes associées : deux polynômes sont égaux (ont même degré et mêmes coefficients) si et seulement si les fonctions polynomiales associées sont égales.

En termes plus abstraits : le morphisme de K-algèbres de K[X] dans qui à un polynôme de K[X] associe la fonction polynomiale , est alors injectif.

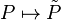
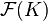
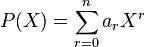
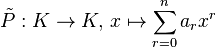
Dans ce cas, il n'y a plus lieu de distinguer le polynôme et la fonction polynomiale associée.

Polynômes particuliers

Les polynômes de

• degré 0 sont appelés fonctions constantes non nulles,
• degré 1 (ou 1) sont appelés fonctions affines,
• degré 2 sont appelés fonctions quadratiques,
• le degré 3 sont appelés fonctions cubiques

La fonction polynôme est un exemple d'une fonction cubique avec comme coefficient dominant -7 et coefficient constant 3.

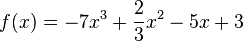
Importance des fonctions polynômes

Les fonctions polynômes sont souvent utilisées parce que ce sont les fonctions les plus simples : leur définition implique seulement l'addition et la multiplication (puisque les puissances ne sont que des sténographies pour les multiplications répétées).

Ils sont aussi simples dans un autre sens : les polynômes de degré inférieur ou égal à n sont précisément les fonctions dont la dérivée (n+1)ième est identiquement nulle.

Un aspect important en calcul numérique est la possibilité d'étudier les fonctions compliquées au moyen d'approximations par des polynômes. Des théorèmes rendent possibles de telles études dans certaines conditions.

Les plus importants sont le théorème de Taylor, qui affirme à peu près que toute fonction n fois différentiable a l'air d'être localement un polynôme, et le théorème d'approximation de Weierstrass, qui affirme que toute fonction continue définie sur un intervalle compact peut être approchée uniformément sur cet intervalle d'aussi près que désiré par un polynôme.

Les quotients de fonctions polynômes sont appelés les fonctions rationnelles. Celles-ci sont les seules fonctions qui peuvent être évaluées directement par un ordinateur, puisqu'à la base, seules les opérations d'addition, de multiplication et de division (et les opérations logiques) peuvent être exécutées par l'unité centrale d'un ordinateur. Toutes les autres fonctions que l'on a besoin d'évaluer à l'aide d'un ordinateur, comme les fonctions trigonométriques, les fonctions logarithmes et les fonctions exponentielles, doivent être alors approchées par des fonctions rationnelles convenables.

Pour évaluer des fonctions polynômes en des valeurs données de la variable x, on n'applique pas le polynôme comme une formule et on ne calcule pas toutes les puissances de x, mais on utilise plutôt la méthode de Horner, beaucoup plus efficace.

Si l'évaluation d'un polynôme en de nombreux points équidistants est demandée, alors la méthode des différences finies de Newton réduit la quantité de travail de façon spectaculaire. Le moteur de différences de Charles Babbage a été conçu pour créer automatiquement de grandes tables de valeurs des fonctions logarithmes et trigonométriques en évaluant des polynômes avec la méthode des différences de Newton, en utilisant beaucoup de points.

Racines

Une racine ou un zéro d'un polynôme P(X) est un nombre r tel que P(r) = 0. Déterminer les racines d'un polynôme de degré supérieur ou égal à 1, ou " résoudre une équation algébrique ", est l'un des plus vieux problèmes mathématiques. Certains polynômes, comme P(X) = X² + 1, n'ont pas de racine dans l'ensemble des nombres réels. Si les racines sont recherchées dans l'ensemble des nombres complexes, alors on pourra en trouver au moins une (ici, il y en a deux.) En effet tout polynôme (non-constant) de admet au moins une racine complexe (voir le théorème de d'Alembert-Gauss.)

Ordre de multiplicité d'une racine

Si r est racine du polynôme P(X), il existe un polynôme Q(X) tel que P(X) = (X − r)Q(X) (pour le démontrer il suffit de retrancher à chaque monôme a_kX^k de P(X) la valeur a_kr^k et de constater que (X − r) se met naturellement en facteur). Si Q(r) est nul, alors on peut encore mettre (X − r) en facteur. On dit alors que r est racine double de P(X).

Plus généralement, s'il existe un polynôme Q(X) et un entier naturel non nul m tels que P(X) = (X − r)^mQ(X) et Q(r)≠0, on dit que r est racine d'ordre m, ou a pour multiplicité m (Q et m sont alors uniques). Par exemple, le polynôme P(X) = X³ − 2X² + X peut aussi s'écrire P(X) = (X − 1)²X ; donc 1 est une racine de P, et sa multiplicité est égale à 2, alors que 0 est racine simple.

Calcul des racines d'un polynôme

La recherche des racines des polynômes de degré 1 ou 2 sont des classiques de l'enseignement pré-universitaire, connus comme "résolution d'une équation du premier ou du second degré". Des formules permettant de calculer les racines des polynômes de degré jusqu'à 4 à partir des coefficients en utilisant les quatre opérations arithmétiques plus les radicaux (racines n-ièmes) étaient déjà connues au seizième siècle (formule de Cardan, de Nicolas Fontana Tartaglia, de Ferrari).

Aucune formule générale de ce type n'existe pour les polynômes de degré 5 ou plus, comme l'a prouvé Abel en 1824. Ce résultat précède de peu la théorie plus générale développée par Galois qui s'engage dans une étude détaillée des relations entre les racines de polynômes.

Les approximations des racines réelles d'un polynôme donné peuvent être trouvées en utilisant la méthode de Newton, ou plus efficacement en utilisant la méthode de Laguerre qui emploie l'arithmétique complexe et permet de localiser toutes les racines complexes. Ces algorithmes sont étudiés en analyse numérique.