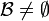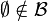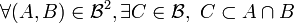Filtre (mathématiques) - Définition

Bases de filtre

Soit E un ensemble et un sous-ensemble de . On dit que est une base de filtre ssi l'ensemble est un filtre. On dit alors que est une base du filtre ou encore que est le filtre engendré par .

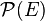
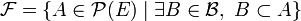
Pour que soit une base de filtre, il faut et il suffit que les trois conditions suivantes soient réalisées :

Filtre convergent, point adhérent à un filtre

Soient E un espace topologique et x un élément de E. On dit que

• un filtre sur E converge vers x s'il est plus fin que le filtre des voisinages de x.
• une base de filtre sur E converge vers x si le filtre qu'elle engendre converge vers x.
• x est adhérent à un filtre (sur E) si tout voisinage V de x et tout élément F de vérifient . Autrement dit il existe un filtre qui contient à la fois et ou encore il existe un filtre plus fin que qui converge vers x.

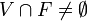
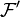
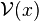
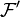
L'ensemble des points adhérents à un filtre est un fermé : c'est .

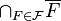
Si un filtre converge vers x alors x est adhérent à . La réciproque est vraie si est un ultrafiltre.

Si E est un espace séparé et que converge à la fois vers x et vers y alors x = y.

Finesse d'un filtre et ultrafiltres

Soit E un ensemble, soit et deux filtres, on dit que est plus fin que si et seulement si .

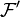
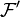
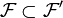
Un ultrafiltre est un filtre maximal pour l'inclusion. En d'autres termes, est un ultrafiltre si et seulement si pour tout filtre plus fin que , on a .

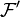
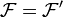
Les filtres principaux sont des ultrafiltres (souvent aussi appelés ultrafiltres triviaux).

Tout filtre est inclus dans un ultrafiltre, Autrement dit, pour tout filtre , il existe un ultrafiltre plus fin que . C'est une conséquence classique de l'axiome du choix ou de son équivalent le lemme de Zorn ; mais, réciproquement, l'axiome du choix s'avère nécessaire pour pouvoir construire des ultrafiltres non principaux (il y a des modèles de ZF dans lesquels il n'en existe pas sur les entiers, par exemple).

Compacité

Les filtres permettent une caractérisation simple des espaces topologiques compacts.

Un espace topologique séparé E est compact ssi tout filtre de E admet un point adhérent, ou encore ssi tout ultrafiltre de E converge.

Cette façon de voir les choses permet de démontrer élégamment le théorème de Tychonov.

Filtre image, limite d'une fonction

Soit E et F deux ensembles, f une fonction de E dans F et un filtre sur E. Le filtre image de par f est par définition l'ensemble des parties de F dont l'image réciproque par f appartient au filtre . Une base de ce filtre est l'ensemble des images directes des éléments de .

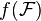
Lorsque que F est un espace topologique et y un élément de F, on dit que f converge vers y suivant si converge vers y.

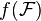
Espace complet - Filtre de Cauchy

Dans un espace uniforme, on peut définir d'une part la notion de filtre de Cauchy et d'autre part la topologie associée à la structure uniforme. On dit alors que l'espace est complet si tout filtre de Cauchy converge.