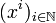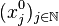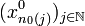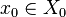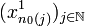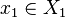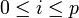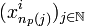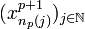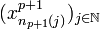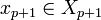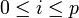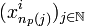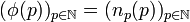Théorème de Tychonov - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le théorème de Tychonov est un théorème de topologie qui affirme qu'un produit d'espaces topologiques compacts est compact au sens de la topologie produit. Il a été publié en 1930 par le mathématicien russe Andreï Nikolaïevitch Tikhonov. Il a plusieurs applications en topologie algébrique et différentielle, particulièrement en analyse fonctionnelle, pour la preuve du théorème de Banach-Alaoglu-Bourbaki et le compactifié de Stone-Čech.
Si ce théorème ne choque pas l'intuition dans le cas d'un produit fini, sa validité dans le cas d'un produit quelconque est plus étonnante, et se démontre par une méthode non constructive faisant appel à l'axiome du choix. On notera qu'il est aussi possible de se passer de l'axiome du choix dans le cas d'un produit dénombrable d'espaces métriques compacts, ce que nous montrons dans la première partie de cet article, la deuxième étant consacrée à la démonstration dans le cas général.
Démonstration dans le cas d'un produit dénombrable de métriques
Dans le cas du produit dénombrable de métriques, l'idée essentielle est de faire de ce produit un espace lui aussi métrique en le munissant d'une distance appropriée, ce qui permet ensuite d'utiliser le théorème de Bolzano-Weierstrass: le produit X sera compact si et seulement si de toute suite d'éléments de X on peut extraire une sous-suite convergente.
Soit donc
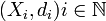
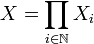
On vérifiera aisément que c'est bien une distance sur X. Montrons qu'elle définit les mêmes ouverts de la topologie produit.
Soit
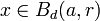
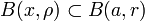
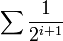
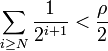
 , si
, si
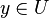
 donc U voisinage au sens de la topologie produit de x inclus dans Bd(a,r): la topologie produit contient donc la topologie métrique.
donc U voisinage au sens de la topologie produit de x inclus dans Bd(a,r): la topologie produit contient donc la topologie métrique.
Réciproquement, soit U ouvert de la topologie produit, soit
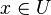
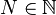
 . On considère alors le rayon
. On considère alors le rayon
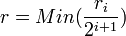
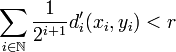
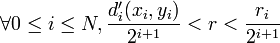
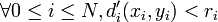
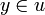
Ainsi, la topologie métrique et la topologie produit sont égales. On peut alors utiliser pour la compacité de X la caractérisation séquentielle par un procédé diagonal: soit