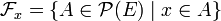Filtre (mathématiques) - Définition

Introduction

La théorie des filtres a été inventée, en 1937, par Henri Cartan et utilisée par Nicolas Bourbaki dans le Livre III : Topologie générale de ses Éléments de mathématique.

Les filtres ont connu la gloire avec la démonstration du théorème de Tychonov dont ils sont la clef.

Avant propos

En mathématiques, la notion de limite est au cœur de nombreux phénomènes et donne lieu à une théorie appelée topologie. Quand on écrit , distinguons deux phénomènes. Le lieu où on calcule la limite, ici, c'est en , et la limite elle-même, ici c'est L. Souvent, on traite les deux problèmes de façon symétrique, en utilisant les voisinages. La définition la plus générale possible se fait dans un espace topologique. On peut en donner une version simplifiée dans un espace métrique.

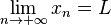
Toutefois, le concept de voisinage se révèle assez vite insuffisant en analyse, même à un niveau très élémentaire. Comment conceptualiser les limites à droites et à gauche par exemple ? On se rend compte sur cet exemple que ce n'est pas tant la limite elle-même que le lieu où on calcule cette limite qui pose problème. Une façon élégante de s'en sortir est d'utiliser un filtre (ou une base de filtre, ce qui est équivalent mais un peu plus souple). La notion de filtre est très générale, elle unifie tous les différents types de limite que l'on rencontre.

Une alternative aux filtres consiste à généraliser le concept de limite d'une suite en utilisant un ensemble ordonné filtrant. Cette alternative (connue sous le nom de convergence des suites généralisées ou de Moore-Smith (en) ) est désormais obsolète et inutile en analyse. Toutefois, on l'utilise dans d'autres domaines. En algèbre, par exemple, elle permet de définir les limites inductives et les limites projectives.

L'intérêt des filtres est de définir la convergence sans avoir besoin de suite ou de fonction.

Exemples

• Soit E un ensemble et x un élément de E. L'ensemble

est un filtre, qu'on dit être un filtre principal en vertu de sa grande simplicité.

• Soit E un espace topologique et x un élément de E. L'ensemble de tous les voisinages de x est un filtre sur E appelé filtre des voisinages de x.

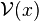
Dans le cas particulier où la topologie de E est discrète, on retombe sur un filtre principal puisque pour la topologie discrète, une partie de E est un voisinage de x ssi elle contient x.

• n'est pas un filtre sur E car il contient l'ensemble vide.

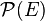
• Le filtre de Fréchet sur un ensemble infini E est l'ensemble des parties de E ayant un complémentaire fini dans E

Définition

Soit E un ensemble, on appelle filtre sur E toute partie de (ensemble des parties de E) tel que :

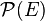
(1) est non vide.

(2) ne contient pas l'ensemble vide.

(3) Toute partie de E contenant un élément de est elle-même un élément de .

(4) Pour tout couple (A,B) de parties de E, si A et B sont dans , est dans .

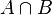
Exemples

• {{x}} est une base du filtre principal
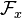
• Soit E un espace topologique et x un élément de E. Une base de voisinages de x est une base du filtre des voisinages de x. On dit aussi système fondamental de voisinages.
• est une base du filtre des voisinages de 0 dans ; en est une autre ; en est encore une autre (cette dernière a l'avantage d'être dénombrable).
• Plus généralement, soit E un espace métrique et x un point de E, l'ensemble des boules ouvertes ou fermées) de centre x et de rayon r>0 est une base du filtre des voisinages de x.
• Dans , est une base du filtre des voisinages épointés de 0, permettant de définir la limite épointée (ou limite par valeurs différentes) d'une fonction en 0.
• Dans , est une base du filtre des voisinages à droite de 0 (épointés), permettant de définir la limite à droite en 0 (ou limite par valeurs strictement supérieures).
• Dans , est une base du filtre de Fréchet, permettant de définir la limite d'une suite.