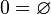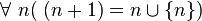Fondements des mathématiques - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Le problème des fondements des mathématiques - Les fondements de l’analyse et la théorie des ensembles - Les fondements de la géométrie - La méthode formelle - Le programme de Hilbert - Les théories des ensembles

Les théories des ensembles

Les mathématiques actuelles sont basées sur la notion d' ensemble. En fait, tout objet mathématique ou presque peut être défini comme un ensemble. Par exemple, « 23 » peut être défini comme un ensemble qui contient 23 éléments.
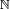
De même, $\ _\mathbb N$ peut être construit à partir d'ensembles comme suit :

$0 = \varnothing$
$\forall\ n ( \ ( n + 1 ) = n \cup \{ n \} )$

(voir à ce sujet l'article sur la construction des entiers naturels).

Avec de telles définitions, ou d’autres semblables, toutes les connaissances mathématiques peuvent être prouvées à l’intérieur d’une théorie des ensembles. Leurs axiomes peuvent être considérés comme les principaux fondements des mathématiques (avec les règles de déduction du calcul des prédicats au premier ordre).

Plusieurs systèmes d’axiomes ont été proposés :

La théorie axiomatique des ensembles « standard » comporte neuf axiomes. Ces axiomes ont été énoncés par Zermelo (1908) et complétés dans les années 1920 par Fraenkel et Skolem. Ils sont dits de Zermelo-Fraenkel et comprennent l'axiome du choix, d'où le sigle ZFC souvent employé pour désigner cette théorie. L'œuvre de l'association Bourbaki a été développée dans ce cadre axiomatique.
La théorie des classes, de von Neumann, Gödel et Bernays (NGB). C’est une extension de ZFC qui lui est presque équivalente. Tous les théorèmes de ZFC sont des théorèmes de NGB. Inversement, tous les théorèmes de NGB qui ne mentionnent que les notions fondamentales de ZFC (c’est-à-dire les ensembles et non les classes) sont des théorèmes de ZFC. NGB convient mieux que ZFC pour formuler la théorie des catégories.

La théorie des types de Whitehead et Russell, exposée principalement dans les Principia Mathematica. Son formalisme est lourd (des dizaines de pages pour prouver des propositions qui nous paraissent au premier abord évidentes) et ses principes sont peu élégants, parce qu’ils imposent beaucoup d’interdits. Outre sa grande importance historique parce qu’elle est la première formulation axiomatique, rigoureuse et cohérente des principes généraux des mathématiques, elle a, grâce à l'informatique, repris de la vigueur à la fin du siècle précédent et au début de celui-ci et devient une discipline phare de la logique mathématique contemporaine.

La théorie du zig-zag interdit de Quine. Elle n'est pas très utilisée mais pourrait l’être davantage. Elle montre en particulier qu’on peut développer une théorie des ensembles sans exclure l’ensemble de tous les ensembles.

D’autres théories, qui sont soit moins puissantes que les précédentes, parce qu’elles refusent les constructions ensemblistes trop audacieuses (théories constructivistes, intuitionnistes, finitaires, ...), soit plus puissantes parce qu’elles les complètent avec d’autres axiomes (axiome de constructibilité, axiomes des très grands ensembles, ...)

Parmi les mathématiciens, certains se contentent des axiomes ZF, et refusent l'axiome du choix (C), car ils considèrent que certaines de ses implications sont contre-intuitives. Certains mathématiciens refusent même ZF et la logique classique qui en est la base, car ils considèrent que tout doit être construit explicitement; c'est la raison pour laquelle on les appelle constructivistes ou intuitionnistes.