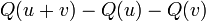Forme quadratique - Définition
La liste des auteurs de cet article est disponible ici.
Généralisations
On peut généraliser la notion de forme quadratique à des modules sur un anneau commutatif. Les formes quadratiques entières sont importantes en théorie des nombres et topologie.
Cas de corps de caractéristique deux
La théorie des formes quadratiques de caractéristique deux possède une petite saveur différente, essentiellement parce que la division par 2 n'est pas possible. Il n'est plus vrai non plus que chaque forme quadratique est de la forme Q(u) = B(u,u) pour une forme bilinéaire symétrique B. En outre, même si B existe, elle n'est pas unique : puisque les formes alternées sont aussi symétriques en caractéristique deux, on peut ajouter toute forme alternée à B et obtenir la même forme quadratique.
Une définition plus générale d'une forme quadratique qui marche pour toute caractéristique est la suivante. Une forme quadratique d'un espace vectoriel V sur un corps F est comme une application
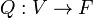
-
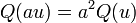
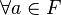
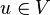
-