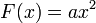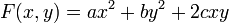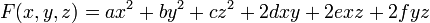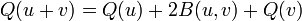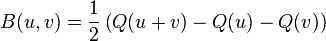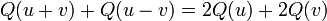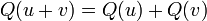Forme quadratique - Définition

Introduction

En mathématiques, une forme quadratique est un polynôme homogène de degré deux avec un nombre quelconque de variables. Par exemple, la distance comprise entre deux points dans un espace euclidien à trois dimensions s'obtient en calculant la racine carrée d'une forme quadratique impliquant six variables qui sont les trois coordonnées de chacun des deux points.

Les formes quadratiques d'une, deux et trois variables sont données par les formules suivantes :

L'archétype de forme quadratique est la forme sur qui définit la structure euclidienne. C'est pourquoi la théorie des formes quadratiques utilise la terminologie de la géométrie (orthogonalité). La géométrie est un bon guide pour aborder cette théorie, malgré quelques pièges.

Les formes quadratiques interviennent dans de nombreux domaines des mathématiques :

• La classification des coniques et plus généralement des quadriques projectives équivaut essentiellement à celle des formes quadratiques sur l'espace vectoriel correspondant.
• Si est une fonction , la partie d'ordre 2 de son développement de Taylor, disons en 0, définit une forme quadratique.

Si 0 est un point critique, cette forme, dans le cas où elle est non dégénérée, permet de décider si on a affaire à un maximum local, à un minimum local ou à un point selle.

• Les formes quadratiques interviennent en mécanique du solide (ellipsoïde d'inertie) et en Statistique (analyse en composantes principales).
• Les formes quadratiques interviennent pour la résolution d'équations diophantiennes, Joseph-Louis Lagrange les utilise pour la démonstration du théorème des deux carrés de Fermat.

Formes quadratiques sur un espace vectoriel

Soit un espace vectoriel V sur un corps F. Pour l'instant, nous supposons que F possède une caractéristique différente de 2. C'est le cas, en particulier, pour les corps réels et complexes qui sont de caractéristique 0. Le cas où la caractéristique vaut 2 sera traité séparément.

Une application Q : est appelée forme quadratique sur V s'il existe une forme bilinéaire symétrique B : telle que

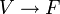
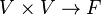
B est alors unique et appelée la forme bilinéaire associée.

En effet, si sont des vecteurs de V,

donc l'expression nécessaire de la forme bilinéaire symétrique B en fonction de Q est:

C'est un exemple de polarisation d'une forme algébrique. Il existe alors une correspondance bijective entre les formes quadratiques sur V et les formes bilinéaires symétriques sur V. À partir d'une forme donnée, nous pouvons définir de manière unique l'autre forme.

Quelques autres propriétés des formes quadratiques :

• et
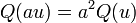
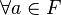
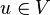
• Q obéit à la règle du parallélogramme :

• Les vecteurs u et v sont orthogonaux par rapport à B ssi

• Pour toute forme quadratique, il existe une base orthogonale, c'est-à-dire

une base telle que pour . C'est une conséquence immédiate de la réduction de Gauss.

Expression matricielle

Si V est de dimension n, et si est une base de V, on associe à B la matrice symétrique B définie par p. La forme quadratique Q est alors donnée par

où les sont les coordonnées de u dans cette base, et u la matrice colonne formée par ces coordonnées. On dit que B est la matrice de Q par rapport à la base.

Q(u) est un polynôme homogène de degré deux par rapport aux coordonnées de u, conformément à notre définition de départ.

Soit une autre base de V, et soit la matrice de passage exprimant les anciennes coordonnées en fonction des nouvelles. De la relation on tire pour la matrice de B dans la nouvelle base. On dit que B et B' sont congruentes.

Rang

Le noyau d'une forme quadratique Q ( on dit aussi radical) est par définition le sous-espace vectoriel

Cet espace est le noyau de l'application linéaire de V dans l'espace dual V* qui associe à x la forme linéaire Une forme quadratique est dite non dégénérée si rad(Q)=0, autrement dit si l'application linéaire ci-dessus est un isomorphisme.

Le rang de Q est par définition dim V - dim(rad(Q)). C'est aussi le rang de la matrice de Q par rapport à une base quelconque.

Sous-espaces orthogonaux

Si W est un sous-espace vectoriel de V, l'orthogonal de W est le sous-espace

Cette notion généralise l'orthogonalité dans les espaces euclidiens, mais il y a quelques pièges. Par exemple sur , la forme quadratique est non dégénérée, mais chacun des sous-espaces et est son propre orthogonal. Plus généralement, si Q est non dégénérée, on a bien , comme dans le cas euclidien. Mais l'intersection n'est pas forcément réduite à zéro.

Discriminant

Soit q une forme quadratique et A sa matrice par rapport à une base de V. Si l'on effectue un changement de base de matrice Q, la matrice de q dans la nouvelle base sera . D'après les propriétés élémentaires des déterminants, . Si q est non dégénérée, l'image du déterminant dans le groupe quotient ne dépend pas de la base. C'est cet élément que l'on appelle le discriminant de la forme quadratique. Si q est dégénérée, on convient que le discriminant est nul.

Exemples

• Corps des complexes

Si , le quotient est réduit à l'élément neutre, et le discriminant est sans intérêt.

• Corps des réels

Si , le quotient s'identifie à , vu comme sous-groupe multiplicatif de . On peut donc parler de formes quadratiques à discriminant positif ou négatif. Par exemple, le discriminant de la forme quadratique ax² + 2bxy + cy² sur , supposée non dégénérée, est donnée par le signe de . S'il est positif, la forme est définie positive ou définie négative, s'il est négatif, la réduction de Gauss sera de la forme . On retrouve, ce qui n'est pas surprenant, la théorie de l'équation du second degré.

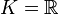
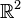
• Corps finis

Si p est un nombre premier, et K le corps à p éléments, la théorie élémentaires des résidus quadratiques assure que est encore isomorphe au groupe à deux éléments.

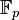
Le problème de classification

On dira que deux formes quadratiques Q et Q' sont équivalentes s'il existe une application linéaire inversible telle que . Il revient au même de dire que leur matrices dans une même base sont congruentes. Classer les formes quadratiques sur un espace vectoriel V c'est

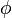
• déterminer les classes d'équivalence de la relation précédente (qui est clairement une relation d'équivalence)
• déterminer les orbites de l'ensemble des formes quadratiques sous l'action du groupe linéaire

donnée par

(ce ne sont que deux façons d'exprimer la même chose).

On a les résultats suivants.

• Si V est un espace vectoriel de dimension finie sur un corps F algébriquement clos

(de caractéristique ) deux formes quadratiques sont équivalentes si et seulement si elles ont même rang. C'est une conséquence directe de la réduction de Gauss

• Si V est un espace vectoriel de dimension finie sur ,

deux formes quadratiques sont équivalentes si et seulement si elles ont même rang et même signature (loi d'inertie de Sylvester).

Deux formes quadratiques équivalentes ont même rang et même discriminant, mais l'inverse est loin d'être en général vrai.