Géométrie dans l'Égypte antique - Définition
La liste des auteurs de cet article est disponible ici.
Le rectangle
Le papyrus de Moscou présente un problème illustrant la parfaite connaissance du calcul de l'aire d'un rectangle :
- Énoncé du problème R6 du papyrus de Moscou
« Exemple de calcul d'un rectangle. Si quelqu'un te dit: Un rectangle de 12 setjat, d'une largeur de 1/2 1/4 sa longueur. Calcule 1/2 1/4 pour avoir 1. Le résultat est 1 1/3. Prends les 12 setjat fois 1 1/3. Le résultat est 16. Calcule sa racine carrée. Le résultat est 4 pour sa longueur. 1/2 1/4 de ceci est 3 pour la largeur. »
- Explication
Ce problème consiste à déterminer la longueur d'un rectangle, le rapport largeur/longueur et l'aire étant fixés.
| Problème posé par le scribe | Transcription du problème en langage algébrique moderne |
| Un rectangle de 12 setjat. | Soit un rectangle dont l'aire est de 12 Setjat (que l'on désigne par B). B = 12. |
| d'une largeur de 1/2 1/4 sa longueur. | Le rapport de la largeur sur la longueur de ce rectangle est de 1/2 + 1/4. soit L cette longueur. la largeur vaut l=L*(1/2+1/4) |
| Calcule 1/2 1/4 pour avoir 1. | Choisis une largeur de 1 et calcule la longueur en faisant l'inverse de 1/2 + 1/4. |
| Le résultat est 1 1/3. | Le résultat est 1 + 1/3, rapport de la longueur sur la largeur. |
| Prends les 12 setjat fois 1 1/3 | Calcule B*(1+1/3) soit L*[L*(1/2+1/4)]*(1+1/3)=L² ce qui revient à transformer le rectangle en carré de côté L. |
| Le résultat est 16. | L² = 16. |
| Calcule sa racine carrée. | Calcule L. |
| Le résultat est 4 pour sa longueur. | L = 4. La longueur du rectangle de 12 setjat est donc 4. |
| 1/2 1/4 de ceci est 3 pour la largeur. | La largeur du rectangle de 12 setjat vaut 4 * (1/2+1/4), soit l=3. |
Le trapèze ou triangle tronqué
L'aire d'un trapèze est parfaitement calculé dans le problème R52 du papyrus Rhind :
« Si on te dit : quelle est l'aire d'un triangle tronqué d'un terrain de 20 khet en sa hauteur, de 6 khet en sa base et de 4 khet en sa ligne tronquée ? Ajoutes sa base à sa ligne tronquée. Cela fait 10. Prends la moitié de 10, 5, de sorte à obtenir un rectangle. Fais 20 fois 5. Cela fait 10. Ceci est sa surface. Calcule comme il suit: »
| 1 | 1000 | |
| 1/2 | 500 | |
| ✔ | 1 | 2000 |
| 2 | 4000 | |
| ✔ | 4 | 8000 |
| | ||
| 10000 (100 setjat) | ||
Méthode équivalente à l'application de la formule
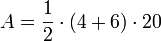
La demi-sphère

L'énoncé M10 du papyrus de Moscou fut étudié maintes fois mais les auteurs ne s'accordent toujours pas sur l'interprétation du problème. Les tenants de l'étude de la surface d'un demi-cercle s'opposent à ceux de l'étude d'une demi-sphère. Il semble bien, aux vues de l'énoncé et en dépit des nombreuses questions que cela engendre, que cette dernière proposition soit la plus acceptable.
- Énoncé du problème M10 du papyrus de Moscou
« Exemple de calcul d'un nbt. Si on te dit : Un nbt dont la base est 4 1/2 entre limites. Peux-tu me faire connaitre sa surface ? Tu feras en sorte de calculer 1/9 de 9. À cause de cela, le nbt est la moitié d'un objet rond, il adviendra 1. Tu feras en sorte de calculer le reste à 8. Tu feras en sorte de calculer 1/9 de 8. Il adviendra 2/3 1/6 1/18. Tu feras en sorte de calculer le reste de ce 8 par rapport à ce 2/3 1/6 1/18. Il advient 7 1/9. Alors, tu feras en sorte de calculer 7 1/9, 4 1/2 fois. Il adviendra 32. Voici sa surface. Tu as trouvé parfaitement. »
Le terme nbt est traduit par corbeille. L'égyptien aboutit donc à un calcul donnant 32 comme résultat. Sylvia Couchoud a remarqué que la formule Aire = (256 / 81) / 2 * d2 de la surface d'une demi-sphère, π étant remplacé par le rapport égyptien 256/81, donne exactement le même résultat.

















































