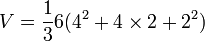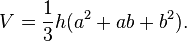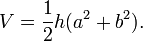Géométrie dans l'Égypte antique - Définition
La liste des auteurs de cet article est disponible ici.
Calcul d'un volume
Autant l'arpentage nécessitait de solides connaissances quant aux calculs des aires, autant la vie domestique et la construction des grands édifices nécessitaient de savoir calculer des volumes, tels que ceux des greniers à blé ou des grandes constructions funéraires.
Volume d'un cube
Comme le montre le problème R44 du papyrus Rhind, la formule du volume d'un solide de forme cubique était connue des anciens Égyptiens : V = l * L * H où l, L et H sont respectivement la longueur, la largeur et la hauteur.
- Énoncé du problème R44 du papyrus Rhind
« Exemple de calcul d'un grenier rectangulaire. Sa longueur est 10, sa largeur est 10 et sa hauteur est 10. Quel montant de grain cela fait-il ? Multiplie 10 par 10. Cela fait 100. Multiplie 100 par 10. Cela fait 1000. Prends la moitié de 1000, soit 500. Cela fait 1500. C'est sa quantité en khar. Prends 1/20 de 1500. Cela fait 75, sa quantité en quadruple-heqat, soit 7500 heqat de grain. »
Volume d'un cylindre (application aux greniers à blé)
Les calculs de volume d'un cylindre interviennent dans les études du contenu des grenier à blé dont la base est ronde. Les représentations égyptiennes de ce type de grenier sont fréquentes (voir ci-contre). Le sommet est de forme ovoïde mais celui-ci n'est jamais pris en compte dans les calculs. L'introduction du grain se faisant par une trappe située au sommet, le tas de grain ne devait jamais dépasser la limite à partir de laquelle le diamètre du grenier diminuait.
Il existe deux types de calcul d'un tel volume. L'exemple suivant présente le premier type, basé sur le calcul de l'aire d'un disque.
- Énoncé du problème R41 du papyrus Rhind
« Exemple de calcul d'un grenier rond dont le diamètre est 9 et la hauteur, 10. Extrait 1/9 de 9, soit 1. Le reste est 8. Multiplie 8 par 8. Cela fait 64. Multiplie 64 par 10. Cela fait 640 coudées (Sous-entendu coudées cubiques). Ajoute la moitié de cela à cela. Cela fait 960: le contenu en khar. Prends 1/20 de 960, soit 48. C'est ce que cela donne en quadruple-heqat de grains, 48 heqat. »
Méthode de calcul :
| 1 | 8 | |
| 2 | 16 | |
| 4 | 32 | |
| ✔ | 8 | 64 |
et
| 1 | 64 | |
| ✔ | 10 | 640 |
| ✔ | 1/2 | 320 |
| | ||
| 960 | ||
| ✔ | 1/10 | 96 |
| ✔ | 1/20 | 48 |
La formule algébrique équivalente serait donc Volumecylindre − en − khar = [(d − (1 / 9) * d)2] * h * (3 / 2), avec d le diamètre du disque et h, la hauteur du cylindre.
Le papyrus Kahun quant à lui, présente un calcul faisant intervenir une seconde méthode :
- Calcul du problème K4 du papyrus Kahun
| ✔ | 1 | 12 |
| 2/3 | 8 | |
| ✔ | 1/3 | 4 |
| | ||
| 16 | ||
et
| ✔ | 1 | 16 |
| ✔ | 10 | 160 |
| ✔ | 5 | 80 |
| | ||
| 256 | ||
et
| ✔ | 1 | 256 |
| 2 | 512 | |
| ✔ | 4 | 1024 |
| ✔ | 1/3 | 85 1/3 |
| | ||
| 1365 1/3 | ||
Ce calcul, répondant au problème du calcul d'un cylindre dont l'énoncé manque, peut être traduit en langage algébrique moderne. L'énoncé devait demander au scribe de calculer le volume en khar d'un grenier rond de 12 coudées de diamètre et de 8 coudées de hauteur.
Nous traduirions le raisonnement du scribe par l'application de cette formule: Volumecylindre − en − khar = (2 / 3) * h * [d + (d / 3)]2, formule strictement équivalente à celle énoncée plus haut reposant sur le calcul de l'aire d'un disque .
Volume d'une pyramide tronquée
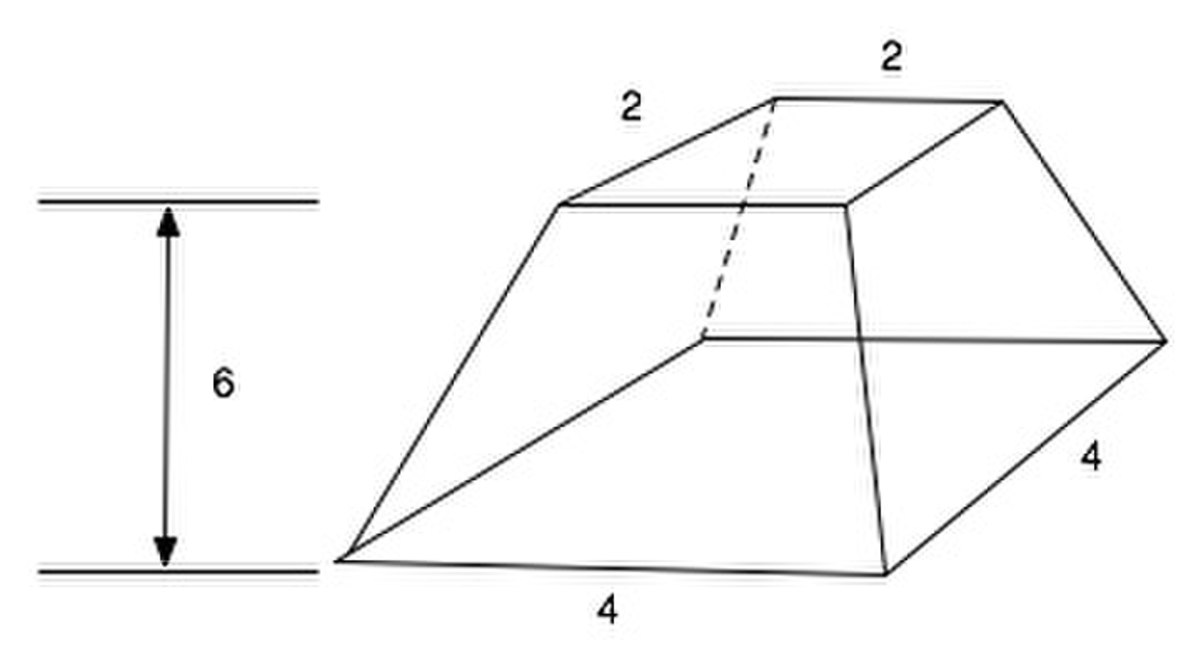
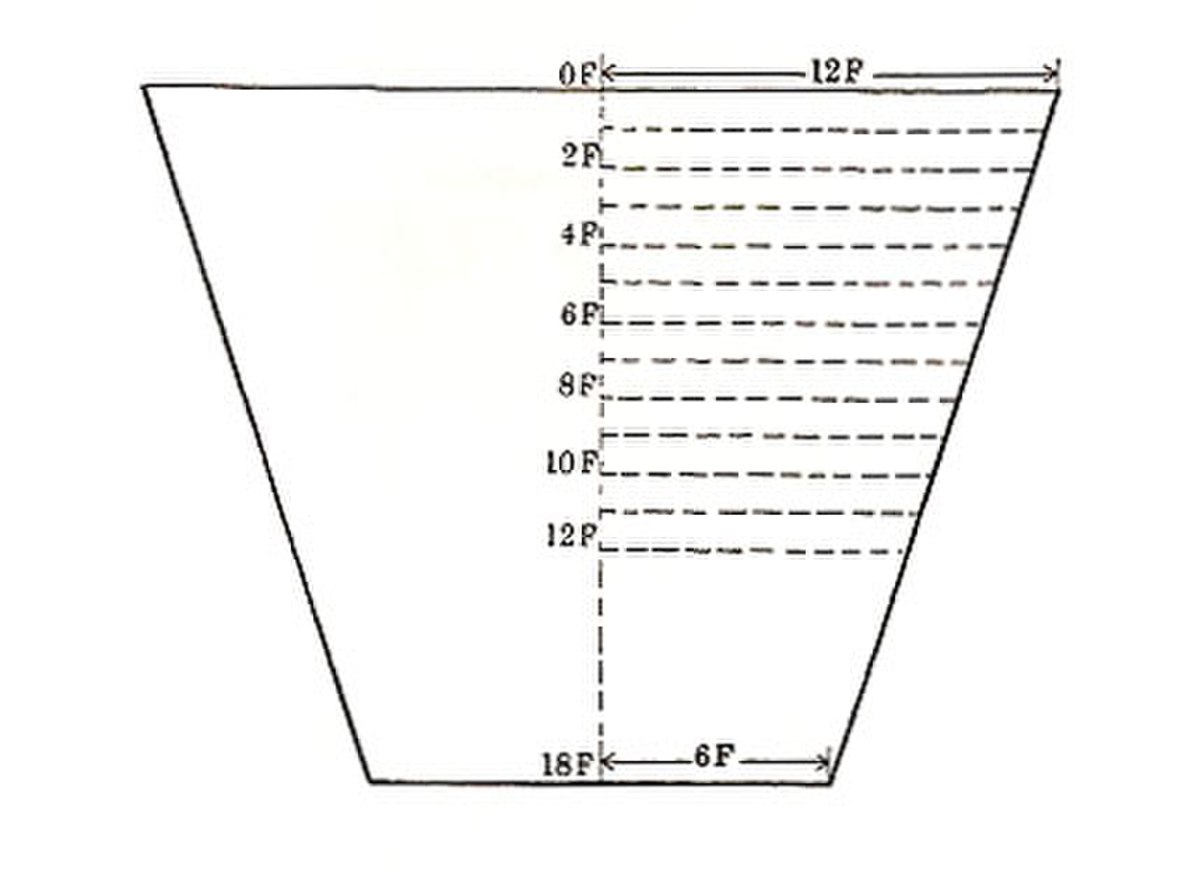
Le problème M14 du papyrus de Moscou est remarquable en ce sens qu'il dévoile l'extraordinaire capacité des anciens Égyptiens à inventer et utiliser des méthodes de calcul complexes et d'une parfaite justesse.
- Énoncé du problème M14 du papyrus de Moscou
« Méthode de calcul d'une pyramide tronquée. Si on te dit : Une pyramide de 6 pour la hauteur par 4 sur la base, par 2 sur le sommet. Calcule le carré de 4. Le résultat est 16. Prends le double de 4. Le résultat est 8. Prends le carré de 2. Le résultat est 4. Tu dois additionner le 16, le 8 et le 4. Le résultat est 28. Prends 1/3 de 6. Il vient 2. Prends 2 fois 28. Il vient 56. Le résultat est 56. Tu trouveras cela correct. »
Cet énoncé décrit le calcul suivant :
que l'on pourrait traduire très exactement par :
formule générale exacte d'une pyramide tronquée.
Le moyen mis en œuvre par les Égyptiens pour déterminer une méthode aussi complexe nous est inconnu. Les babyloniens eux-mêmes ne sont parvenus qu'à une approche approximative du résultat pouvant être associée à la formule suivante :
Volume d'un tronc de cône
Un papyrus d'époque tardive, mais découvert en Égypte à Oxyrhynque traite du volume d'un tronc de cône identifié à une clepsydre. La description de cet instrument rappelle de très près la clepsydre de Karnak et démontre que les anciens Égyptiens furent très tôt capables de calculer de tels volumes.