Géométrie dans l'Égypte antique - Définition
La liste des auteurs de cet article est disponible ici.
Le cercle et l'ellipse
Le calcul de l'aire d'un disque représente sans doute l'un des progrès les plus significatifs effectué en mathématiques par les anciens égyptiens. Il est également l'un des exercices qui a fait couler le plus d'encre, le nombre pi et la quadrature du cercle semblant intimement liés au problème. Le calcul de l'aire est ainsi traité dans les problèmes R41, R42, R43, R48 et R50 du papyrus Rhind et enfin le problème M10 du papyrus de Moscou.
- Énoncé du problème R50 du papyrus Rhind
| 1 | 9 | |
| ✔ | 1/9 | 1 |
« Soustrais-le, il reste 8 »
| 1 | 8 | |
| 2 | 16 | |
| 4 | 32 | |
| ✔ | 8 | 64 |
« La surface du champ est 64 setjat. »
La formule appliquée par la scribe est donc clairement : Aire = (d − (1 / 9) * d)2, d étant le diamètre du disque. L'énoncé évoque un champ rond de 9 khet, étant sous-entendu que 9 khet est le diamètre.
Cette formule est équivalente à celle-ci: Aire = (64 / 81) * d2. La formule moderne du calcul de l'aire d'un disque étant πr2 ou (π / 4)d2, la plupart des auteurs attribuent aux anciens Égyptiens l'approximation de la valeur π à 256/81 soit 3,1605, valeur remarquable pour l'époque. Cependant, le problème R50 exposé ci-dessus ne prouve pas que les Égyptiens aient eu conscience de l'existence de cette constante. La seule certitude est qu'ils pouvaient calculer l'aire d'un disque à partir de son diamètre, et d'en donner une valeur approchée avec une grande précision en l'assimilant à un carré. La méthode employée pourrait bien trouver une explication dans une esquisse géométrique du problème R48 du papyrus Rhind.
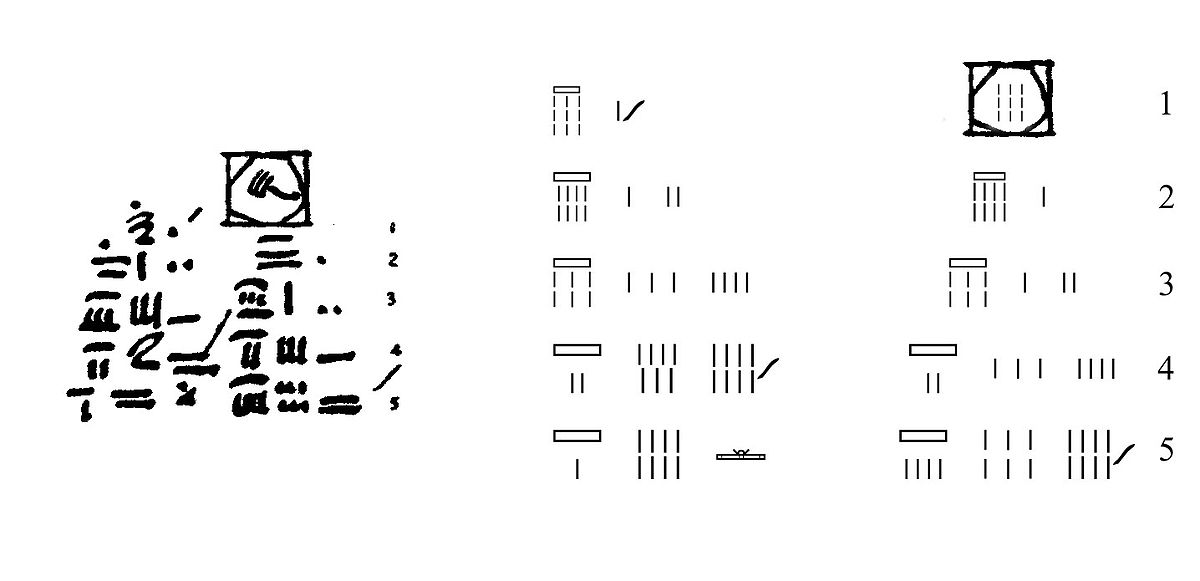
- Opérations du problème R48 du papyrus Rhind
| 1 | 8 setjat | |
| 2 | 16 setjat | |
| 4 | 32 setjat | |
| ✔ | 8 | 64 setjat |
et
| ✔ | 1 | 9 setjat |
| 2 | 18 setjat | |
| 4 | 36 setjat | |
| ✔ | 8 | 72 setjat |
| | ||
| 81 | ||
Le problème ne contient aucun énoncé, ce qui rend son interprétation délicate. Néanmoins, son intérêt réside dans l'esquisse accompagnant les opérations mathématiques décrites ci-dessus. Celle-ci représente un cercle maladroitement dessiné (ou bien une figure octogonale) inscrit dans un carré. À l'évidence, les calculs sont relatifs à l'aire du disque de diamètre 9, comparable à celui du problème R50.
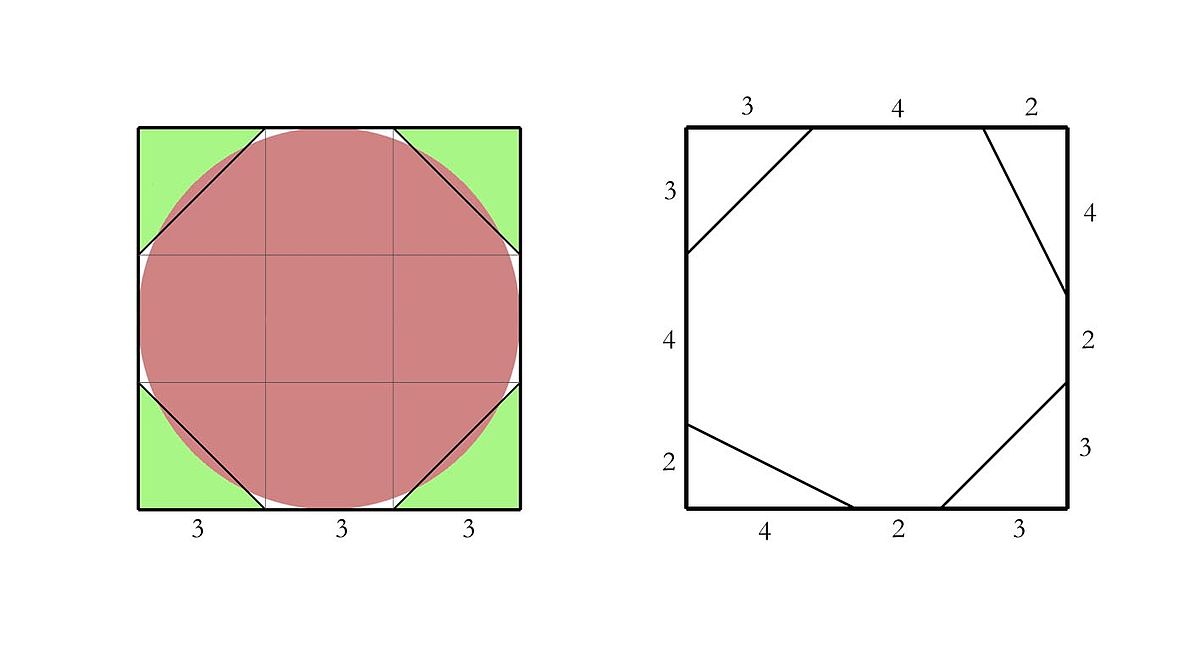
La première hypothèse concernant ce dessin est que le scribe considère le disque dont il cherche l'aire comme équivalent à un octogone. Ce dernier est ainsi inscrit dans un carré dont les côtés sont égaux au diamètre du disque. L'octogone ayant une aire de 9² - 2 * 3² = 63, la surface du disque est alors approximée à 64.
La deuxième hypothèse, avancée par Michel Guillemot, reproduit plus fidèlement le dessin et considère que la surface du disque est équivalente à un octogone irrégulier dont l'aire est exactement de 9² - (3² + 2*4) = 64 (voir figure ci-dessous). Cet auteur est allé plus loin en émettant l'hypothèse que le scribe pouvait reconstituer un carré de côté 8 en décomposant cet octogone, ce qui revient à avancer que l'idée de quadrature du cercle était déjà présente à leur esprit. Cette dernière hypothèse a toutefois le mérite de donner une explication satisfaisante à la formule utilisée au problème R50, qui revient à avancer l'égalité entre l'aire d'un disque et l'aire d'un carré dont les côtés sont égaux au 8/9e du diamètre du disque.
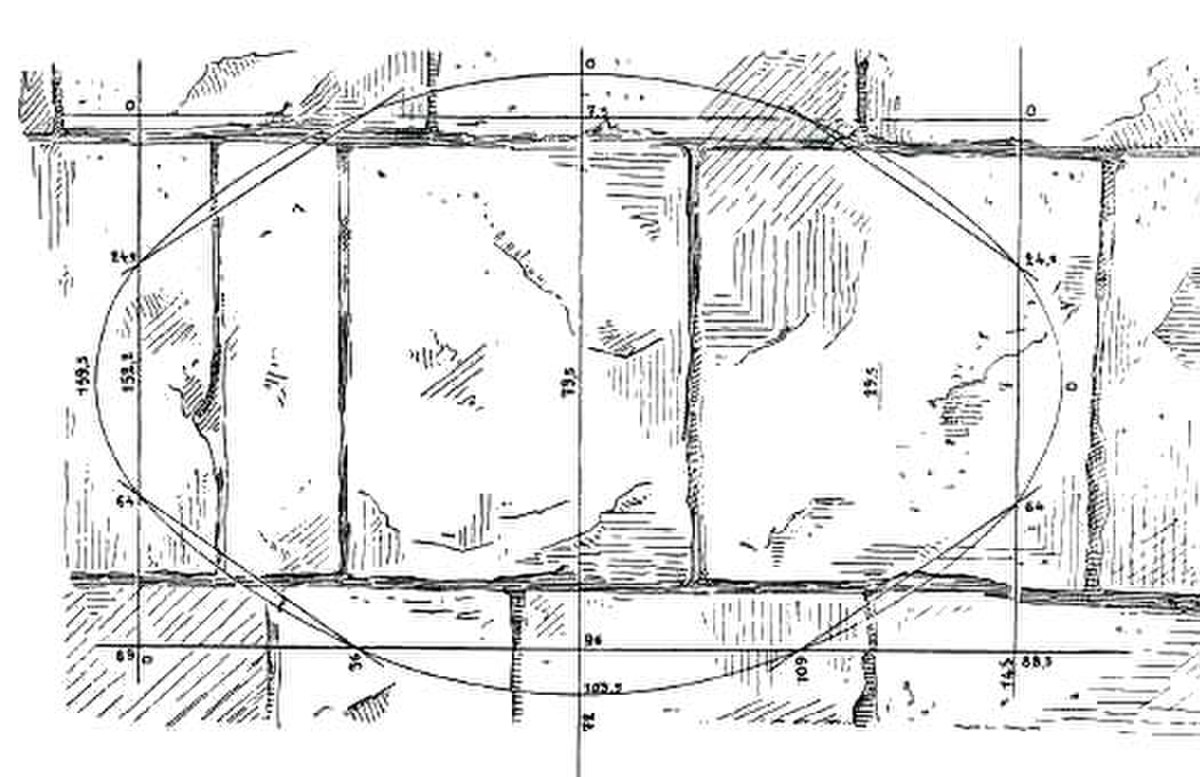
Cette recherche géométrique pourrait trouver un équivalent dans une autre esquisse, découverte sur un mur du temple de Louxor par Ludwig Borchardt. Il s'agit d'une ellipse construite à l'aide d'un rectangle, les aires des deux figures n'étant différentes que de 1%.
.