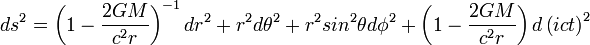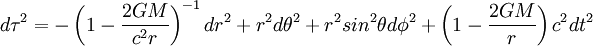Géométrie de Schwarzschild - Définition

Expression de la métrique de Schwarzschild

On a donc satisfait aux conditions fixées, ce qui permet d’écrire la métrique de façon complète et compatible avec les lois de la gravitation newtonienne :

On trouve aussi l’écriture suivante

où la vitesse de la lumière est c = 1 et où l’intervalle de temps propre dτ remplace l’élément de longueur ds. Parfois la lettre s est utilisée à la place de τ dans la relation précédente οù ds est un intervalle de temps et non un intervalle d’espace. Ces unités réduites ne permettent pas de faire des vérifications grâce aux équations aux dimensions ; il est préférable d’utiliser le système international SI.

Nous avons obtenu la métrique de Schwarzschild par diverses considérations de symétrie et par la nécessité d’être en accord avec la loi de la gravitation de Newton pour les mouvements circulaire et radial. La déviation de la lumière par le Soleil et la précession du périhélie de Mercure se produisent dans de faibles champs de gravitation mais ne sont pas prévisibles par la mécanique newtonienne car la trajectoire du photon dévié par le Soleil comme celle de Mercure n'est ni rectiligne ni circulaire. Einstein avait obtenu ces résultats avant l'apparition de la métrique de Schwarzschild grâce à des approximations judicieuses. On trouvera une démonstration plus complète dans l'article "Métrique de Schwarzschild" et ailleurs.

. La métrique de Schwarzschild, solution exacte des équations d'Einstein, remplace donc la loi de la gravitation universelle de Newton pour expliquer ces deux phénomènes.