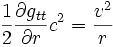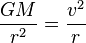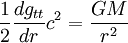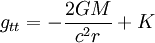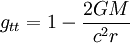Géométrie de Schwarzschild - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La géométrie de Schwarzschild est définie par sa métrique. Pour l'obtenir, on peut résoudre les équations d'Einstein complètes en symétrie sphérique et en statique. Nous nous contenterons ici d'un calcul simplifié avec une métrique de Minkowski à l'infini, en appliquant le principe de correspondance et utilisant l'invariant de volume d'espace-temps d'Einstein, qui s'interprète à partir de la relativité restreinte où dilatation du temps et contraction de la longueur sont inverses l'une de l'autre.
L’équation générale de la métrique est exprimée sous forme diagonale car on peut toujours effectuer une rotation pour diagonaliser la matrice représentative de la métrique dans ses axes principaux :
Symétrie sphérique
L’espace est supposé homogène et isotrope, la solution doit être invariante dans une rotation. La rotation sur une sphère s'exprime, en fonction de la colatitude et de la longitude sous la forme :
Le rayon de la sphère ne variant pas, on peut multiplier par r2, ce qui donne la métrique
Les coefficients de la métrique gθθ et gφφ ne sont pas modifiés dans une rotation sur la sphère de rayon r.
Métrique de Minkowski à l’infini
La métrique de Minkowski s’écrit en coordonnées sphériques :
On doit la retrouver à grande distance de la source de gravitation, c’est-à-dire à l’infini où on doit avoir grr = gtt = 1
Métrique statique
Les coefficients grr et gtt de la métrique doivent être indépendants du temps, c’est-à-dire que leurs dérivées partielles par rapport au temps doivent être nulles. Ils ne dépendent donc que de la distance r à l’astre :
Il n’y a donc pas d’ondes gravitationnelles dans ce modèle. La transmission des efforts y est instantanée selon la loi de l’action et de la réaction.
Equation du déterminant
En relativité restreinte, la dilatation du temps est exactement l'inverse de la contraction de la longueur. On retrouve cette propriété en relativité générale en résolvant les équations d'Einstein d'une métrique statique. C'est la conservation du volume d'espace-temps d'Einstein où le déterminant de la métrique doit être égal à un. L’espace-temps se déforme sans changement de volume, la quatrième dimension étant la dimension spatiale représentée par le nombre imaginaire ict. Cette condition évite aussi que le déterminant ne devienne infini si gtt ou grr le devient. Cette « symétrie » gttgrr = 1 donne le second coefficient de la métrique :
Principe de correspondance
On doit retrouver la loi de l’attraction universelle de Newton lorsque vitesse et gravitation sont faibles. Cette condition va nous donner gtt grâce à une orbite circulaire dans un plan équatorial où ϑ = 0 donc aussi dϑ = 0. Le rayon étant constant, Dr = 0 le coefficient grr n’intervient pas. On obtient une métrique simplifiée, où grr n’apparaît pas
Sur la géodésique, le lagrangien formé à partir de la métrique est unitaire
où
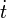
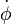
La vitesse (en fait la dérivée
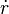
Effectuons la dérivation, puis L = 1 et
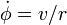
Après simplification on obtient l’équation :
Pour trouver la métrique, on doit identifier cette équation avec son homologue newtonienne en exprimant l’égalité des accélérations de gravitation et centripète :
On obtient, en identifiant les deux relations précédentes :
Cette équation différentielle s’intègre en
où K est une constante d’intégration. On doit avoir gtt = 1 à l’infini pour retrouver la métrique de Minkowski, d’où K = 1. Le coefficient de d(ict)2 est donc :
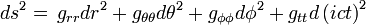
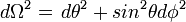
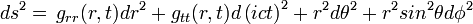
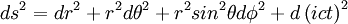
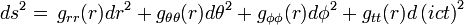
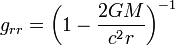
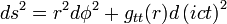
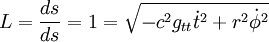
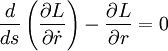
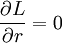
![\frac{\partial L}{\partial r}=\frac{-\frac{\partial g_{tt}}{\partial r}c^2\dot t^2+2r\dot \phi^2}{2\sqrt{-c^2g_{tt}\dot t^2+r^2\dot \phi^2}}=-\frac12\frac{\partial g_{tt}}{\partial r}c^2\dot t^2+2r\dot \phi^2=\left[-\frac12\frac{\partial g_{tt}}{\partial r}c^2+r \left(\frac{v}{r}\right)^2\right]\dot t^2](https://static.techno-science.net/illustration/Definitions/autres/5/5b2e29f1226ffb16e94b34c0b9b8851d_ebd6ae1ae06eb600c2af44ee6a04974b.png)