Groupe cyclique - Définition

Morphisme

Endomorphisme

Soit G un groupe cyclique d'ordre n, g un générateur et ψ un endomorphisme. La structure de G est entièrement déterminée par l'élément g. En conséquence, ψ est entièrement déterminé par l'image de g.

Soit p l'entier tel que ψ(g) = g ^p.

Réciproquement, si p est un entier (que l'on peut choisir entre 1 et n), alors l'application ψ qui à g^k associe g ^p.k définit un endomorphisme.

En effet :

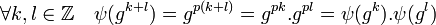
On en déduit les premières propriétés sur les endomorphismes des groupes cycliques :

• Un endomorphisme sur un groupe cyclique est entièrement déterminé par l'image d'un générateur.
• Il existe exactement n endormorphismes sur un groupe cyclique d'ordre n.

L'analyse de la fonction indicatrice d'Euler montre que:

• Il existe exactement φ(n) automorphismes d'un groupe cyclique d'ordre n dans lui-même, si φ désigne l'indicatrice d'Euler.

On peut remarquer, dans le cas où l'ensemble d'arrivée est différent de l'ensemble de départ, que si le groupe de départ est cyclique, alors l'image du morphisme est aussi cyclique.

Caractère

Un caractère est un morphisme d'un groupe dans le groupe multiplicatif (C^*,·) des éléments non-nuls du corps des nombres complexes. Cette notion est au cœur d'une théorie importante, celle des représentations d'un groupe fini.

• Il existe exactement n caractères pour un groupe cyclique d'ordre n.
• L'image d'un caractère est l'ensemble des racines pièmes de l'unité, où p est le cardinal de l'image. On remarquera alors que p divise n.

En conséquence, tout caractère a pour image un groupe, sous-groupe de l'ensemble des racines nièmes de l'unité, où n est le cardinal du groupe. De plus, l'ensemble des racines nièmes de l'unité forme un groupe cyclique.

• Soit g un générateur du groupe cyclique et r une racine nième de l'unité, alors il existe un et un seul caractère ψ tel que l'image de g par ψ soit égal à r. De plus, ψ est défini par l'égalité suivante :

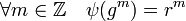
• Soit g un générateur du groupe cyclique et r une racine nième de l'unité, alors il existe un et un seul caractère ψ tel que l'image de g par ψ soit égal à r. De plus, ψ est défini par l'égalité suivante :

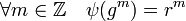
L'image d'un générateur détermine entièrement le caractère. En effet, pour tout élément du groupe, il existe un entier m tel que g^m est égal à cet élément. De plus, l'application définie par l'égalité précécente est clairement un morphime. La proposition est donc bien démontrée.

• Il existe exactement n caractères pour un groupe cyclique d'ordre n.

C'est une conséquence directe de la proposition précédente.

• L'image d'un caratère est l'ensemble des racines pièmes de l'unité, où p est le cardinal de l'image.

L'image d'un générateur par un caractère engendre un sous-groupe, soit p son cardinal. Le théorème de Lagrange démontre que tout élément de l'image est une racine pième de l'unité et que p divise n. Or, il existe exactement p racines de l'unité, ces racines forment donc l'image du caractère et la proposition est démontrée.

 

Propriétés

Théorème chinois

Le théorème chinois permet la décomposition d'un groupe cyclique fini en groupes cycliques plus petits et, en général, plus simples. Ce théorème est largement utilisé en théorie algébrique des nombres et plus spécifiquement en arithmétique modulaire. Il est aussi à la base de nombreux algorithmes de cryptographie, on peut citer par exemple celui qui est utilisé dans le cryptage RSA. En théorie des groupes, le théorème s'énonce de la manière suivante :

• Soient u et v deux entiers premiers entre eux, alors le groupe cyclique d'ordre u.v est isomorphe au produit des groupes cycliques d'ordre u et v.

Note : Si u et v ne sont pas premiers entre eux, alors le groupe produit ne contient pas d'élément d'ordre supérieur au ppcm de u et de v. Ce groupe n'est donc pas isomorphe au groupe cyclique d'ordre u.v.

Ce théorème entraine une décomposition unique d'un groupe cyclique en facteurs premiers, si n est l'ordre du groupe alors le théorème fondamental de l'arithmétique montre que n se décompose de la manière unique suivante:

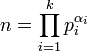
Ou (p_i) est une famille de k nombres premiers tous distincts et α_i des entiers supérieurs ou égaux à un. Les puissances des nombres premiers du produit sont tous premiers entre eux. Une simple récurrence montre :

• Tout groupe cyclique se décompose de manière unique en un produit de groupes cycliques d'ordre une puissance d'un nombre premier.

• Montrons que si u et v sont premiers entre eux, alors les groupes sont isomorphes.

Soit G (respectivement G_u et G_v) un groupe cyclique d'ordre u.v (respectivement u et v) et d'élément générateur g (respectivement g_u et g_v). Soit φ l'application de G dans G_u x G_v définie par :

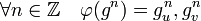
Remarquons ensuite que φ est un morphisme:

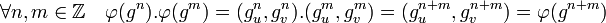
Remarquons enfin φ est bijective : En effet, si g^m est élément du noyau, alors m est un multiple de u et de v. Comme ces deux nombres sont premiers entre eux, on en déduit que m est un multiple de u.v. Donc g^m est l'élément neutre de l'ensemble de départ, et φ est injective car son noyau est réduit à l'élément neutre. Comme les groupes de départ et d'arrivée ont le même cardinal et que l'application est injective, elle est aussi surjective. Nous avons montré que φ est bijective.

Conclusion : φ est un morphisme bijectif du groupe cyclique vers le groupe produit, les deux groupes sont donc bien isomorphes.

• Montrons que si u et v ne sont pas premiers entre eux, alors le groupe produit ne contient pas d'élément d'ordre supérieur au ppcm de u et de v.

Notons p le ppcm de u et de v. La puissance pième d'un élément quelconque de G_u (respectivement G_v) est égal à l'élément neutre d'après le théorème de Lagrange. En effet, p est un multiple de l'ordre des groupes. On en déduit que la puissance pième d'un élément quelconque du groupe produit est égal à l'identité. On en conclut que le groupe produit ne contient pas d'élément d'ordre supérieur à p.

En revanche, G contient par définition un élément d'ordre u.v qui est strictement plus grand que p. Les deux groupes ne peuvent donc pas être isomorphes.

 

Indicatrice d'Euler

Le nombre d'éléments générateurs d'un groupe cyclique correspond à une question importante. Elle intervient par exemple dans les calculs de déterminations des polynômes cyclotomiques ou dans la fonction zêta de Riemann. Cette fonction est en général notée φ et si n est un entier, φ(n) désigne le nombre d'éléments générateurs d'un groupe cyclique d'ordre n.

La valeur de l'indicatrice d'Euler s'obtient par l'expression de l'ordre u du groupe donnée par le théorème fondamental de l'arithmétique :

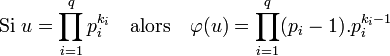
Dans la formule, p_i désigne un nombre premier et k_i un entier strictement positif. Une démonstration est proposée dans l'article détaillé.

Dans le groupe cyclique Z/nZ, si l'on note ses éléments {0, 1, 2,..., n-1}, alors les générateurs sont les k qui sont premiers avec n et leur nombre est une autre définition de l'indicatrice d'Euler.