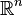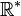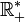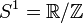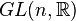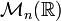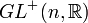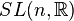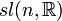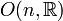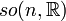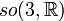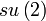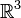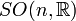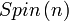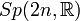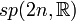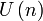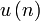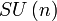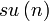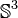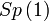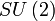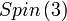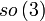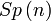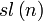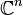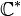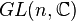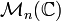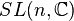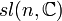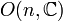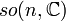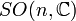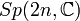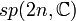Groupe de Lie - Définition

Exemples

Groupes de Lie réels (groupes de Lie classiques)

Groupe de Lie	Description	Propriétés	Algèbre de Lie	Description	Dimension
	Espace euclidien muni de l'addition	Abélien; Simplement connexe, non compact		Le crochet de Lie est nul	n
	Nombres réels non nuls munis de la multiplication	Abélien; Non connexe, non compact		Le crochet de Lie est nul	1
	Nombres réels strictement positifs munis de la multiplication	Abélien; Simplement connexe, non compact		Le crochet de Lie est nul	1
	Nombres complexes de module 1 munis de la multiplication	Abélien; Connexe, non simplement connexe, compact		Le crochet de Lie est nul	1
	Groupe général linéaire : matrices réelles n×n inversibles	Non connexe, non compact		Matrices n×n, le crochet de Lie étant le commutateur	n²
	matrices réelles n×n à déterminant positif	Simplement connexe, non compact		Matrices n×n, le crochet de Lie étant le commutateur	n²
	Groupe spécial linéaire : matrices réelles de déterminant 1	Simplement connexe, non compact si n > 1		Matrices carrées de trace nulle, le crochet de Lie étant le commutateur	n²-1
	Groupe orthogonal : matrices orthogonales réelles	Non connexe, compact		Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur; est isomorphe à et muni du produit vectoriel	n(n - 1)/2
	Groupe spécial orthogonal : matrices orthogonales réelles de déterminant 1	Simple et semisimple pour n=3 et n≥5; Connexe, compact, non simplement connexe pour n≥2		Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur	n(n - 1)/2
	Groupe Spin	Simple et semisimple pour n=3 et n≥5; Simplement connexe, compact		Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur	n(n - 1)/2
	Groupe symplectique : matrices symplectiques réelles	Simple, semisimple; Non compact		Matrices réelles satisfaisant JA + ATJ = 0 où J est la matrice antisymétrique standard	n(2n + 1)
	Groupe unitaire : matrices unitaires n×n complexes	Non simplement connexe, compact; Isomorphe à S1 pour n=1		Matrices carrées complexes A vérifiant A=-A*, le crochet de Lie étant le commutateur	n²
	Groupe spécial unitaire : matrices unitaires complexes n×n de déterminant 1	Simple et semisimple pour n≥2; Simplement connexe, compact		Matrices carrées complexes de traces nulles A vérifiant A=-A*, le crochet de Lie étant le commutateur	n²-1
	Quaternions de module 1 munis de la multiplication, également noté	Simple, semisimple; Simplement connexe, compact; Topologiquement une sphère, isomorphe à et		Quaternions de partie réelle nulle, le crochet de Lie étant le produit vectoriel; Isomorphe aux vecteurs réels de dimension 3, également isomorphe à et	3
	Groupe compact symplectique : matrices unitaires n×n quaternioniques	Simple, semisimple; Compact, simplement connexe		Matrices quaternioniques carrées A vérifiant A=-A*, le crochet de Lie étant le commutateur	n(2n + 1)

Groupes de Lie complexes

Les dimensions sont données sur . (Tout groupe ou algèbre de Lie complexe peut être vu comme un groupe ou une algèbre de Lie réel de dimension double.)

Groupe de Lie	Description	Propriétés	Algèbre de Lie	Description	Dimension
	Espace euclidien muni de l'addition	Abélien; Simplement connexe, non compact		Le crochet de Lie est nul	n
	Nombres complexes non nuls munis de la multiplication	Abélien; Non simplement connexe, non compact		Le crochet de Lie est nul	1
	Groupe général linéaire : matrices complexes n×n inversibles	Simplement connexe, non compact; Isomorphe à pour n=1		Matrices n×n, le crochet de Lie étant le commutateur	n²
	Groupe spécial linéaire : matrices complexes de déterminant 1	Simple, semisimple; Simplement connexe, non compact pour n≥2		Matrices carrées de trace nulle, le crochet de Lie étant le commutateur	(n²-1)
	Groupe orthogonal : Matrices orthogonales complexes	Non connexe, non compact pour n≥2		matrices antisymétriques carrées complexes, le crochet de Lie étant le commutateur	n(n-1)
	Groupe spécial orthogonal : matrices orthogonales complexes de déterminant 1	Simple et semisimple pour n=3 et n≥5; Non simplement connexe, non compact pour n≥2		Matrices antisymétriques carrées complexes, le crochet de Lie étant le commutateur	n(n-1)
	Groupe symplectique : matrices symplectiques complexes	Simple et semisimple; Non compact		Matrices complexes satisfaisant JA+ATJ=0 où J est la matrice antisymétrique standard	2n(2n+1)

Groupes de Lie quaternioniens

Les dimensions sont données sur .

Groupe de Lie	Description	Propriétés	Algèbre de Lie	Description	Dimension
	Quaternions non nuls munis de la multiplication	Simplement connexe, non compact		Quaternions, le crochet de Lie étant le commutateur	1

Groupes de Lie exceptionnels

On répertorie 5 groupes de Lie dits exceptionnels, notés respectivement E6, E7, E8, F4 & G2