Groupe de Lie - Définition

Algèbre de Lie associée à un groupe de Lie

Il est possible d'associer naturellement à tout groupe de Lie G une algèbre de Lie. Il existe deux manières équivalentes d'introduire cette algèbre de Lie. L'une consiste à introduire un espace de champs de vecteurs sur G, la seconde consiste à munir l'espace tangent en l'élément neutre d'un crochet de Lie, dérivant de l'expression locale de la loi interne de G.

Comme algèbre de champs de vecteurs

G désigne un groupe de Lie réel ou complexe de dimension n. Pour g un élément de G, l'application L_g : G G définie par L_g(f) = gf est un difféomorphisme de la variété réelle ou complexe sous-jacente à G. Un champ de vecteurs X sur G est dit invariant à gauche lorsque pour tout couple d'élément g et h de G, on a : dL_g(X_h) = X_gh (où on note X_a la valeur du champ de vecteurs X au point a).

Pour toute variété différentielle réelle ou complexe M, l'espace vectoriel réel ou complexe des champs de vecteurs sur M, noté I(M), est muni d'une structure naturelle d'algèbre de Lie réelle ou complexe, dont le crochet est le crochet de champs de vecteurs. La naturalité signifie exactement que tout morphisme f:M N entre variétés induit un morphisme d'algèbres de Lie f* : I(N) I(M). En particulier, pour M = N = G, on dispose d'automorphismes (L_g)* de l'algèbre de Lie I(G). L'ensemble des points fixes communs à tous ces automorphismes (L_g)* est une sous-algèbre de Lie de I(G), notée g. Ses éléments sont les champs de vecteurs invariants à gauche sur G.

Comme espace tangent

Soit T_eG l'espace tangent en e à G, e désignant l'élément neutre de G. L'application (où X_e est la valeur de X en l'élément neutre) est un isomorphisme linéaire. La structure d'algèbre de Lie de g se transporte donc, via cet isomorphisme, en une structure d'algèbre de Lie sur l'espace vectoriel T_eG

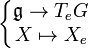
Cette structure peut se définir directement. Supposons donnée f une carte locale de G en l'élément neutre e avec f(e)=0, alors, l'application produit lue dans la carte locale f est au second ordre près :

f(f^-1(a).f^-1(b))=a+b+B(a,b)+...

où B est une forme bilinéaire antisymétrique. La structure d'algèbre de Lie sur T_eG est donnée par :

[X,Y] = B(X,Y).

Application exponentielle

Dans la première présentation, tout vecteur X de g est par définition un champ de vecteurs invariant à gauche sur G. L'invariance à gauche implique que son flot est globalement défini. L'exponentielle de X est définie comme l'image au temps 1 de l'élément neutre e de G. Plus précisément, il existe une unique fonction dont la dérivée est donnée par :

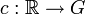
et telle que c(0) = e.

Elle possède la propriété remarquable suivante :

pour tous s et t.

Si l'on note, pour v = X_e, e^v = c(1), une reparamétrisation incluant la variable t montre que :

.

On peut alors vérifier :

.

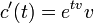
Cette fonction est également appelée fonction exponentielle et relie l'algèbre de Lie g au groupe de Lie G. Elle définit un difféomorphisme entre un voisinage de 0 dans g et un voisinage de e dans G. Toutefois, en général, l'application exponentielle n'est pas surjective, ni injective.

Un sous-groupe à un paramètre de G est une application différentiable c G vérifiant l'identité eq.2 ci-dessus. À tout sous-groupe à un paramètre c est associé un unique élément X de g vérifiant : c(t) = e^tv.

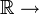
Classification algébrique des groupes de Lie

Plusieurs groupes de Lie peuvent partager la même algèbre de Lie associée. Cependant, à toute algèbre de Lie g correspond un groupe de Lie simplement connexe G, unique à isomorphisme près. De plus cet isomorphisme est uniquement déterminé par l'isomorphisme d'algèbre de Lie associé. Tout groupe de Lie connexe dont l'algèbre de Lie est isomorphe à g se réalise comme quotient de G par un sous-groupe normal discret.

Un groupe de Lie connexe est simple, semisimple, résoluble, nilpotent ou abélien si et seulement si son algèbre de Lie associée possède la propriété de même nom. En particulier, la classification des algèbres de Lie semi-simples donne une classification des groupes de Lie simplement connexes et semi-simples.