Groupe des unités - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Motivation - Exemples - Définitions et propriétés

Définitions et propriétés

Groupe des unités

Dans un anneau unifère, un élément est dit inversible si, par définition il admet un inverse pour la loi de multiplication. On parle aussi d'unité de l'anneau. L'ensemble des éléments inversibles d'un anneau A est appelé groupe des unités ou groupe des inversibles. Cet ensemble, noté U(A), est une partie de A stable par multiplication et passage à l'inverse. La multiplication de A induit donc une loi de groupe sur U(A).

Quand l'anneau est un corps, on parle aussi parfois du groupe multiplicatif.

L'image d'une unité par un homomorphisme d'anneaux unifères est inversible. Par conséquent, un homomorphisme d'anneaux unifères f de A dans B induit un morphisme de groupes de U(A) dans U(B). En théorie des catégories, on interprète ce fait en disant que U est un foncteur de la catégorie des anneaux unifères dans la catégorie des groupes, mais oublions.

En particulier, si C est un sous-anneau unifère de A, alors son groupe des unités U(C) est un sous-groupe de U(A).

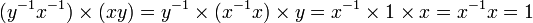
U(A) est stable par produit et passage à l'inverse: Si x est inversible dans A, il possède un inverse y ; et y possède alors un inverse dans A, qui est précisément x ! Donc, l'inverse d'un élément inversible est inversible.; Si x et y sont des unités de A, alors y^-1x^-1 est un inverse de xy. En effet, l'associativité donne:; $(y^{-1}x^{-1})\times (xy)=y^{-1}\times (x^{-1}x)\times y=x^{-1}\times 1\times x=x^{-1}x=1$ .; Par conséquent, le produit de deux inversibles est inversible.; L'associativité de la multiplication est garantie par les propriétés de l'anneau et l'existence d'un élément neutre par le fait que l'anneau est choisi unifère.
L'image d'un inversible est inversible: Soit un élément inversible x d'un anneau unifère A. Notons y l'inverse de x dans A. Soit un homomorphisme d'anneaux unifères f de A dans B. Comme xy = 1 dans A, il vient : f(x)f(y) = f(xy) = 1. Par conséquent, f(x) est inversible dans B (et son inverse est f(y)).

Divisibilité

(Si l'anneau est non commutatif, il y a une construction similaire en intervertissant partout droite et gauche ; s'il est commutatif, les deux constructions coïncident).

Dans un anneau unifère, x est dit associé à y si il existe un inversible u tel que x = uy. C'est une relation d'équivalence. On peut remarquer que le groupe des unités U(A) agit sur A par multiplication à gauche. Les orbites de cette action de groupe sont précisément les classes d'éléments associés.

Il existe une relation de préordre appelée divise définie de la manière suivante :

x divise y (à droite) si et seulement s'il existe un élément a de l'anneau tel que y = ax.

(C'est une relation binaire réflexive et transitive.)

La relation d'association est compatible avec la relation "divise" au sens où :

Pour x et v associés, pour y et w associés, alors x divise y ssi v divise w.

Pour un anneau intègre, si x divise y et y divise x alors x et y sont associés. Par passage au quotient, la division induit alors une relation d'ordre sur les classes d'éléments associés.

La relation est associé à est reflexive car si x est un élément de l'anneau x = 1x, elle est symétrique car si y est un élément de l'anneau et u une unité tel que x = u. y, alors y = u^-1.x (l'anneau est supposé commutatif), enfin elle est transitive car si x, y et z sont des éléments de l'anneau tel qu'il existe u et v dans le groupe des unités avec x = u.y et y = vz, alors x = uv z et uv est inversible. Elle est donc une relation d'équivalence.

Soit x et y deux éléments de l'anneau, si x est associé à y alors x divise y et y divise x, la relation d'association est bien compatible avec la relation de division. De plus si x divise y et si y divise x alors il existe deux éléments u et v tel que y = ux et x = vy ce qui montre que x = uvx. Si x est nul alors y = ux = 0 = x. Si x est non nul, comme l'anneau est intègre, uv est égal à 1 donc u et v sont des unités. En conclusion x est associé à y, ce qui montre que la relation de division sur le quotient de l'anneau est antisymétrique. Enfin si x divise y et si y divise z alors il existe a et b éléments de l'anneau tel que y = ax et z = by donc z = abx et la relation est transitive. En conclusion la relation de division est une relation d'ordre sur le quotient de l'anneau par la relation d'association.

L'application du quotient de l'anneau par la relation d'association, muni de la relation "divise", dans l'ensemble des idéaux principaux à gauche de l'anneau, ordonné par la relation "contient" est un isomorphisme.

Cette proposition signifie deux propriétés : deux éléments a et b de l'anneau engendrent le même idéal à gauche si, et seulement si, a et b sont associés, de plus Aa contient Ab si, et seulement si, a divise b.