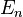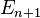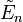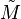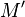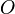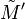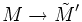Homologie (transformation géométrique) - Définition

Introduction

Homologie

Il n'existe apparemment aucun rapport entre les homologies géométriques vues dans cet article, et les groupes d'homologie en topologie différentielle.

Définition

Les homologies (vectorielles, affines, projectives) d'un espace (vectoriel, affine, projectif) sont les bijections (linéaires, affines, projectives) de cet espace dans lui même ayant un hyperplan invariant point par point, appelé la base de l'homologie, ou son axe en dimension 2.

En dimension finie, toute bijection (linéaire, affine, projective) est composée d'un nombre fini d'homologies (vectorielles, affines, projectives) ; autrement dit ces dernières sont des générateurs du groupe (linéaire, affine, projectif).

Homologies affines

Les homologies affines ayant un point fixe, on retrouve exactement les deux cas : dilatation, et transvection.

Homologies vectorielles

Nous allons voir qu'elles sont constituées des dilatations et des transvections.

Soit f une homologie d'un espace vectoriel  ; est donc un hyperplan, et est donc une droite, stable par  ; la restriction de à est donc une homothétie de rapport  ; on a alors deux cas :

1. et sont en somme directe : est une affinité vectorielle de base , de direction et de rapport  ; dans ce cas où la base est un hyperplan, on parle de dilatation.
2. est inclus dans  : si est un vecteur directeur de , on montre qu'il existe alors une forme linéaire de noyau telle que pour tout de  :

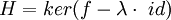
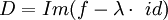
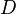
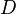
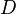
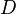
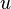
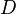
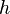
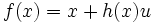
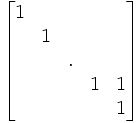
Une telle application est appelée une transvection.

Homologie par perspective

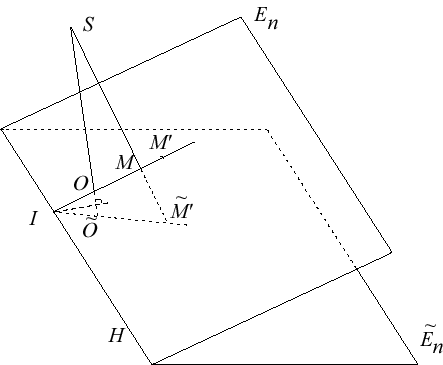Plongeons l'espace euclidien de dimension n comme hyperplan d'un espace de dimension n+1 et faisons tourner autour de son hyperplan , de façon à en obtenir une copie . Tout point de a une copie dans , donc aussi l'image de par une homologie projective de base et de centre du complété projectif de . On montre que les droites joignant à passent par un point fixe , de sorte que l'application est la restriction d'une projection centrale de centre S. On remarque que se trouve sur la droite passant par et orthogonale à l'hyperplan bissecteur de et .

Homologies projectives

Soit une homologie de l'espace projectif , de base un hyperplan . On sait que le complémentaire de peut être muni d'une structure d'espace affine (les droites parallèles dans sont les droites de sécantes en un point de ). La restriction de à est alors une application affine qui transforme une droite en une droite parallèle.

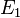
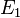
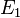
Les homologies projectives sont donc les complétées projectives des translations et des homothéties.

• Les homologies complétées d'une translation sont dites spéciales, ou appelées élations ; le point à l'infini de la translation est appelé leur centre.
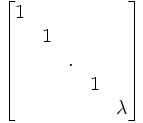
• Les homologies complétées d'une homothétie sont dites générales : leur centre et rapport sont ceux de l'homothétie ;
• Les homologies de rapport -1 (complétées d'une symétrie centrale) sont dites harmoniques.

Les droites passant par le centre d'homologie sont globalement invariantes, et cette propriété est caractéristique : Une homographie est une homologie ssi elle possède un point fixe tel que les droites passant par ce point sont globalement invariantes.

Étant donnés deux points et en dehors d'un hyperplan , il existe une unique homologie de base et transformant en  ; les constructions sont indiquées ci-dessous :

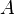
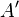
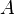
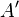
Homologie générale de rapport λ
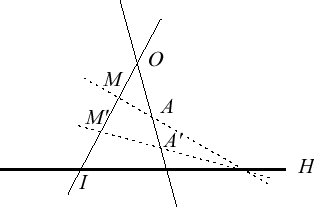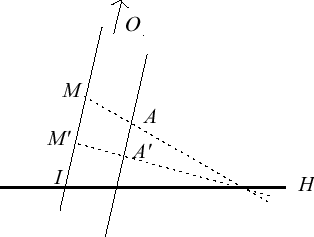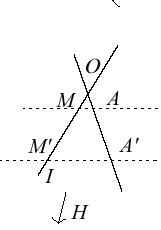Cas où le centre et la base sont à distance finie. Le birapport (O,I,M,M') est constant égal à λ.	Cas où la base est à distance finie, et le centre à l'infini : la restriction au complémentaire d'un hyperplan contenant le centre est une dilatation de rapport 1 / λ	Cas où la base est à l'infini, et le centre à distance finie : la restriction au complémentaire de la base est une homothétie de rapport λ

Homologie spéciale ou élation
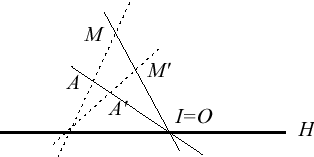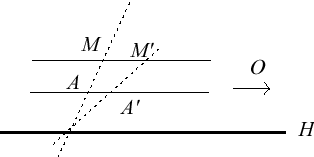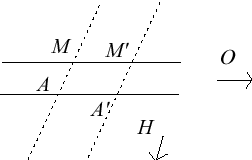Cas où le centre et la base sont à distance finie.	Cas où la base est à distance finie, et le centre à l'infini : la restriction au complémentaire d'un hyperplan contenant le centre est une transvection.	Cas où la base est à l'infini (et donc le centre aussi) : la restriction au complémentaire de la base est une translation.

Point de vue algébrique : l'espace projectif E étant défini comme l'ensemble dont les points sont les droites vectorielles de l'espace vectoriel , les homologies projectives de E sont les homographies provenant des homologies vectorielles de  ; en dimension finie, les homologies générales de rapport λ ont pour matrice homogène réduite et les homologies spéciales : .