Dilatation - Définition
La dilatation est l'expansion du volume d'un corps occasionné par son réchauffement, généralement imperceptible. Dans le cas d'un gaz, il y a dilatation à pression constante ou maintien du volume et augmentation de la pression.
Coefficients de dilatation thermique α
Formules générales : cas isotrope
On peut calculer pour tous les matériaux isotropes la variation de longueur et donc de volume en fonction de la variation de température :
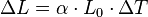
Avec :
-
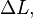
-
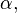
-
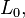
-
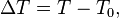
Remarque : Puisque l'on utilise une variation, une différence de température, la différence d'origine entre Kelvin et degré Celcius s'annule, la distinction n'est donc pas nécessaire.
On peut aussi directement calculer la longueur en fonction de la température :
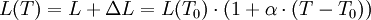
Avec :
-
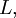
-
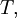
-
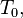
Application
Soit un rail en acier de 30 m en hiver à -20°C ; en été, la température est de 40°C.
Le rail subit donc un variation de température
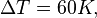
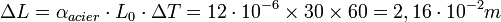
Ainsi le rail s'allonge de 21,6 mm, sa longueur en été est de 30,0216 m.
Tenseur de dilatation thermique
Les matériaux cristallins non cubiques présentent une dilatation thermique anisotrope : on n'observe pas le même coefficient de dilatation

Ainsi, dans le cas général d'un matériau triclinique, six coefficients de dilatation thermique sont nécessaires. Ces coefficients se rapportant à un repère orthogonal, les coefficients de dilatation n'ont pas forcément de rapport direct avec les axes cristallographiques du matériau. En effet, les valeurs propres et vecteurs propres d'un tenseur d'ordre 2 forment toujours (dans le cas où les valeurs propres sont positives) une ellipsoide de révolution, dont les axes sont perpendiculaires les uns aux autres : on dit qu'un tenseur d'ordre 2 possède toujours au moins la symétrie ponctuelle orthorhombique maximale
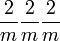
Pour un cristal orthorhombique par exemple, où
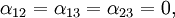
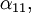
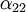
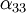
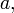


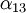
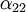
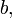
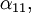
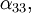
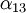
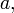
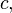
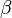
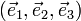
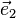
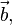
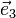
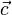
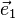
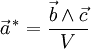
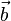
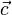
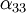
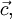
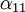
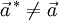
Les valeurs propres du tenseur de dilatation thermique, ou coefficients de dilatation linéaires principaux
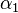
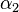
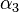
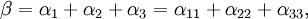
Mesure des coefficients de dilatation linéaires
Dans le cas des matériaux cristallins, la dilatation thermique se mesure de façon précise par diffraction des rayons X. Une méthode couramment utilisée consiste à mesurer les paramètres de maille du cristal pour différentes températures et d'en déduire les coefficients de dilatation linéaires. Cependant, le calcul intermédiaire des paramètres de maille introduit des erreurs supplémentaires dans le calcul des coefficients et il est préférable de les obtenir à partir de la variation en température de l'angle de diffraction
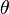
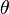
Coefficients de dilatation linéaires pour les principaux matériaux
Les coefficients donnés ci-dessous sont valables pour des températures comprises entre 0°C et 100°C. En réalité ces coefficients dépendent de la température, la loi d'allongement n'est donc pas linéaire pour des différences de température très élevées.
| substances | coefficient de dilatation linéaire 1/K |
|---|---|
| acier | 12,0×10−6 |
| aluminium | 23,8×10−6 |
| argent | 19,7×10−6 |
| bismuth | 13,5×10−6 |
| bronze | 17,5×10−6 |
| cadmium | 30,0×10−6 |
| constantan | 15,2×10−6 |
| cuivre | 16,5×10−6 |
| étain | 23,0×10−6 |
| fonte | 10,5×10−6 |
| invar (36 %Ni + 64 %Fe) | 1,5×10−6 |
| laiton | 18,5×10−6 |
| maillechort | 18,0×10−6 |
| substances | coefficient de dilatation linéaire 1/K |
|---|---|
| molybdène | 5,2×10−6 |
| nickel | 13,0×10−6 |
| nylon | 130×10−6 |
| or | 14,2×10−6 |
| platine | 9,0×10−6 |
| plomb | 29,0×10−6 |
| porcelaine | 4,0×10−6 |
| quartz | 0,5×10−6 |
| rilsan | 150×10−6 |
| tungstène | 4,5×10−6 |
| verre | 9×10−6 |
| zinc | 30,0×10−6 |
Anomalies
- L'eau présente une anomalie ; en effet en chauffant elle se contracte entre 0°C et + 4°C.
Problèmes dus à la dilatation
La dilatation des solides est compensée sur les ponts par des rainures : avec les différences d'expositions au soleil et l'échauffement de l'atmosphère, un solide de plusieurs dizaines de mètres peut s'allonger de quelques centimètres. Sans l'espace laissé par les rainures, le pont se déformerait.
- La dilatation d'un liquide est souvent négligeable par rapport à son ébullition, mais peut expliquer certains phénomènes, notamment avec des récipients rigides.
- Elle n'est pas la cause du débordement du lait que l'on chauffe trop, qui est un phénomène propre aux protéines bouillies.
- Le bris des verres chauffés brusquement s'explique par la dilatation.
- Blocage de roue. Si une roue est d'une matière différente de celle de son axe, elle pourra se bloquer à certaines température si les tolérances mécaniques ont été mal calculées.
Applications de la dilatation
- Thermomètre bi-lame
- Thermoscope
- Dilatomètre
Personnalités ayant travaillé sur la dilatation
- Louis Joseph Gay-Lussac decouvreur de la loi de dilatation des Gaz
- Pierre Louis Dulong
- Charles Edouard Guillaume, prix Nobel de physique (1920), découvrit des alliages ayant de faibles coefficients de dilatation.