Inégalité de Hoeffding - Définition
La liste des auteurs de cet article est disponible ici.
L’inégalité de Hoeffding est une inégalité de concentration concernant les sommes de variables aléatoires indépendantes et bornées. Il existe une version plus générale de cette inégalité, concernant une somme d'accroissements de martingales, accroissements là encore bornés : cette version plus générale est parfois connue sous le nom d'inégalité d'Azuma-Hoeffding.
Inégalité de Hoeffding — Soit une suite
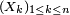
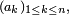
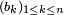
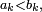
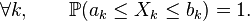
On pose
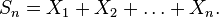
Alors, pour tout 
![\begin{align} \mathbb{P}\left(S_n-\mathbb{E}[S_n]\ge t\right) &\le\exp\left(-\frac{2\,t^2}{\sum_{i=1}^n(b_i-a_i)^2}\right), \\ \mathbb{P}\left(S_n-\mathbb{E}[S_n]\le -t\right) &\le\exp\left(-\frac{2\,t^2}{\sum_{i=1}^n(b_i-a_i)^2}\right), \\ \mathbb{P}\left(\left|S_n-\mathbb{E}[S_n]\right|\ge t\right) &\le 2\exp\left(-\frac{2\,t^2}{\sum_{i=1}^n(b_i-a_i)^2}\right). \end{align}](https://static.techno-science.net/illustration/Definitions/autres/d/dd8d4f6a4175d7a8f16fb22bcc43946c_195fec7b4df2ef9b1ac28770aebe1853.png)
La démonstration fait usage de la proposition suivante :
Proposition — Soit
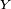
![\scriptstyle\ \mathbb{E}[Y]=0\](https://static.techno-science.net/illustration/Definitions/autres/7/79eafb8ba68d587b62b98e058f29ae22_d65bb214cbd4a2f3efc94a3edc87a58c.png)
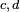
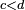
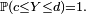

![\mathbb{E}\left[e^{sY}\right]\le\exp\left(s^2(d-c)^2/8\right).](https://static.techno-science.net/illustration/Definitions/autres/6/6960962fffebfd110beeb689d5f15cb1_46efceb40d12a47c8d82da35478dfa6d.png)
Par convexité de la fonction
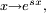
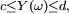
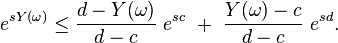
En passant à l'espérance, puisque
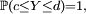
![\mathbb{E}[e^{sY}]\le f(s)=\frac{d}{d-c}\ e^{sc}\ +\ \frac{-c}{d-c}\ e^{sd}.](https://static.techno-science.net/illustration/Definitions/autres/b/be6bb4e5a10ccbb14dcb4fa52f6bc018_2041f2cb23d3a31814894896bd278138.png)
On pose
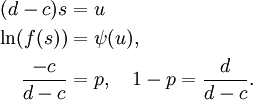
Il suit que
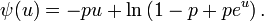
On remarque alors que
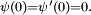
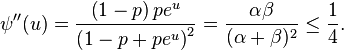
Alors, en vertu de la formule de Taylor-Lagrange,
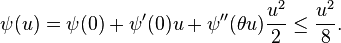
On pose alors
![\begin{align} Y_{i}&=X_{i}-\mathbb{E}[X_{i}], \\ c_{i}&=a_{i}-\mathbb{E}[X_{i}],\quad d_{i}=b_{i}-\mathbb{E}[X_{i}], \end{align}](https://static.techno-science.net/illustration/Definitions/autres/d/d1659cb54eaa573c46a9ea74a950c4e3_231399de7cb2c6a69ccc1e46f2da3e5f.png)
et on remarque que
![\begin{align} \mathbb{P}(c_i\le Y_i\le d_i)&=1, \\ d_{i}-c_{i}&=b_{i}-a_{i}, \\ S_{n}-\mathbb{E}[S_{n}]&=Y_{1}+Y_{2}+\dots+Y_{n}. \end{align}](https://static.techno-science.net/illustration/Definitions/autres/0/07cc41c8b075391be2db49238eb3e907_d2af4067bcd52dd5de892874d441f70b.png)
Pour tout  on a donc, en vertu d'un corollaire de l'inégalité de Markov, de l'indépendance des
on a donc, en vertu d'un corollaire de l'inégalité de Markov, de l'indépendance des
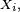
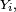
![\begin{align} \mathbb{P}\left(S_n-\mathbb{E}[S_n]\ge t\right) &\le\mathbb{E}\left[e^{s(S_n-\mathbb{E}[S_n])}\right]e^{-st} \\ &=\mathbb{E}\left[e^{s(Y_{1}+Y_{2}+\dots+Y_{n})}\right]e^{-st} \\ &=e^{-st}\ \prod_{i=1}^n\mathbb{E}\left[e^{sY_{i}}\right] \\ &\le\exp\left(-st+\frac{s^2\ \sum_{i=1}^n(b_i-a_i)^2}8\right). \end{align}](https://static.techno-science.net/illustration/Definitions/autres/0/0f0e5b1f7b7b034f0856258332518b4b_e24c863f0e7cb3972931a11e655df02d.png)
L'inégalité est en particulier vraie pour
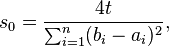
qui réalise le minimum de la borne de droite, ce qui démontre la première inégalité. La deuxième inégalité se démontre en remplaçant
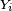
![\scriptstyle\ Y^{\prime}_{i}=\mathbb{E}[X_{i}]-X_{i},\](https://static.techno-science.net/illustration/Definitions/autres/8/860c03ec1f5bf88b6911190816d2a3ba_1523ea3f605d5cdc1fa65e1046708000.png)
![\scriptstyle\ S_{n}-\mathbb{E}[S_{n}]\](https://static.techno-science.net/illustration/Definitions/autres/5/51a77424e5a6b92376a865ada98e358d_1abf2800eda6c1e63b8f29dd2cbb4f9d.png)
![\scriptstyle\ \mathbb{E}[S_{n}]-S_{n},\](https://static.techno-science.net/illustration/Definitions/autres/2/2cc7002b81478216baf2b93661d5f779_c8253d085f4a5a9e835b1a8aa6c310a9.png)
![\begin{align} c^{\prime}_{i}&=\mathbb{E}[X_{i}]-b_{i}, \\ d^{\prime}_{i}&=\mathbb{E}[X_{i}]-a_{i}, \end{align}](https://static.techno-science.net/illustration/Definitions/autres/3/3354210215851cec0add36b39be12458_b03ddf70f0b24c4c527a5831d7cc330c.png)
et en remarquant que
![\begin{align} \mathbb{P}(c^{\prime}_i\le Y^{\prime}_i\le d^{\prime}_i)&=1, \\ d^{\prime}_{i}-c^{\prime}_{i}&=b_{i}-a_{i}, \\ \mathbb{E}[S_{n}]-S_{n}&=Y^{\prime}_{1}+Y^{\prime}_{2}+\dots+Y^{\prime}_{n}. \end{align}](https://static.techno-science.net/illustration/Definitions/autres/f/f8a9e86aadb109d92a5fd0a8a78dee5a_68d7692251e61daf7f661c95acdc2488.png)
La troisième inégalité est une conséquence directe des deux premières.
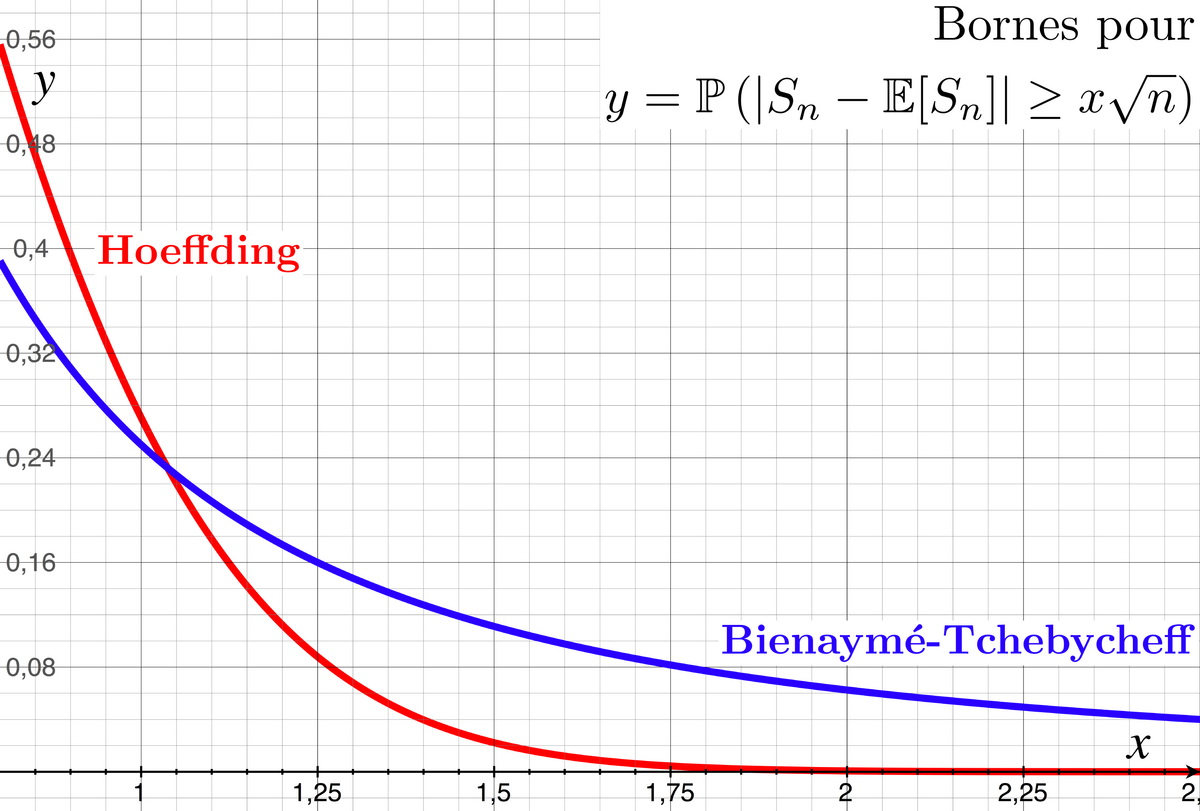
Supposons que
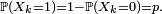
Alors
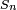
![\begin{align} \mathbb{P}\left(\left|S_n-\mathbb{E}[S_n]\right|\ge x\sqrt{n}\right) &\le \frac{p(1-p)}{x^2}, \\ \mathbb{P}\left(\left|S_n-\mathbb{E}[S_n]\right|\ge x\sqrt{n}\right) &\le 2\exp\left(-2\,x^2\right). \end{align}](https://static.techno-science.net/illustration/Definitions/autres/8/86f871cfe1a0dc696c50651e387dbe4c_553908577cba949f722a3d1ae14fdcb6.png)
On voit que dans ce cas (et c'est assez représentatif de la situation générale) l'inégalité de Hoeffding est beaucoup plus précise pour


















































