Dispersion - Définition

Introduction

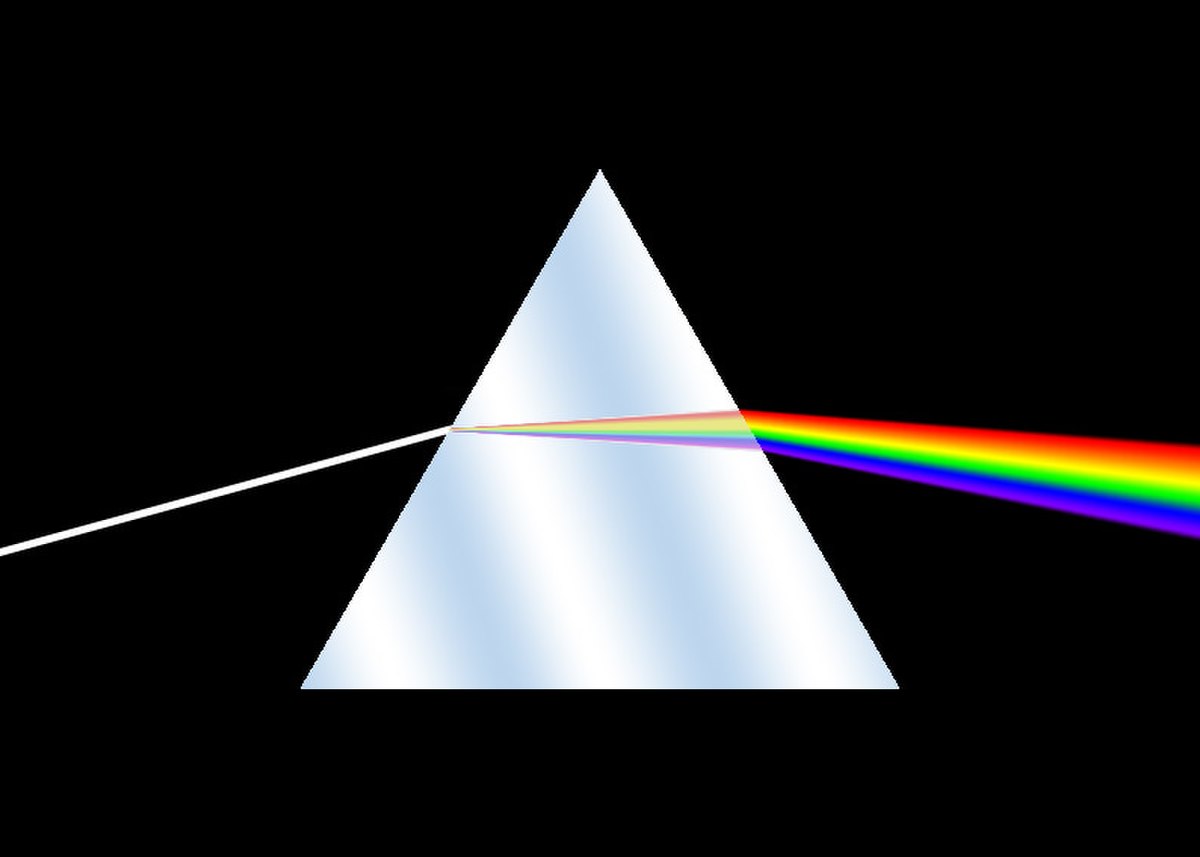
La dispersion, en mécanique ondulatoire, est le phénomène affectant une onde dans un milieu dispersif, c'est-à-dire dans lequel les différentes fréquences constituant l'onde ne se propagent pas à la même vitesse. On rencontre ce phénomène pour tous types d'ondes, comme la lumière, le son ou les vagues. Les arcs-en-ciel sont une manifestation de la dispersion induite par l'atmosphère.

Le vide n'est pas dispersif pour les ondes lumineuses: la vitesse de la lumière ne dépend pas de sa fréquence.

Ondes dans un milieu dispersif

Une onde sinusoïdale est caractérisée par sa fréquence ν ou sa pulsation ω = 2πν (en rad/s), et par son vecteur d'onde de norme k = 2π / λ (en rad/m), où λ est la longueur d'onde.

On observe alors qu'il existe deux vitesses caractéristiques différentes :

• la vitesse de phase qui correspond au déplacement des fronts d'onde ;
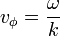
• et la vitesse de groupe qui correspond au déplacement de l'enveloppe de l'onde, ou autrement dit, de l'énergie.

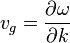
Ces deux vitesses ont alors des comportements différents selon le type de milieu.

• Si le milieu est non-dispersif, c'est-à-dire v_φ ne dépend pas de k, alors ω est forcément proportionnel à k. On obtient donc que les deux vitesses sont égales, et constantes.
• Si le milieu est dispersif, ces deux vitesses ne sont alors plus égales, et dépendent de k.

Ces propriétés sont remarquables dans l'étude de la propagation d'un paquet d'onde : c'est, par définition, une superposition de plusieurs ondes sinusoïdales de différentes longueurs d'onde. On peut montrer que sa vitesse correspond à la vitesse de groupe.

Dans un milieu non dispersif, comme v_g = v_φ, la vitesse du paquet d'ondes est la même que les ondes sinusoïdales qui le composent. L'animation suivante illustre ce phénomène :

Les ondulations serrées, à l'intérieur du paquet d'onde, se déplacent en bloc sans se déformer (l'ondulation la plus haute au centre du paquet reste en son centre).

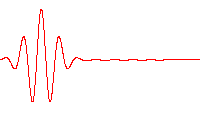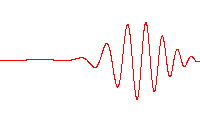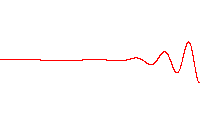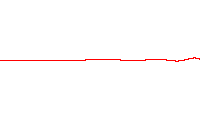
Dans un milieu dispersif, le paquet d'onde ne va pas à la même vitesse que les ondes qui le composent, comme le montre l'animation suivante :

Les ondulations serrées défilent à l'intérieur du paquet, parce qu'elles avancent moins vite que la forme du paquet.

La dispersion dans d'autres domaines de la physique

La dispersion intervient dans tous les types d'ondes en physique. On peut citer par exemple les vagues lorsque le fond de la mer n'est pas plat, les ondes de plasma, le son, les arcs-en-ciel, etc.

En optique

Variation de l'indice de réfraction

Un milieu est caractérisé par son indice de réfraction n = c/v, où c est la célérité de la lumière dans le vide et v sa vitesse dans le milieu considéré. Une variation de cet indice sur le trajet d'un rayon lumineux va causer sa déviation, ou plutôt réfraction selon les lois de Snell-Descartes.

Ainsi, lorsque le milieu de propagation est dispersif, la vitesse de propagation, et donc l'indice de réfraction dépendent de la fréquence : la déviation des rayons dépend de la fréquence, c'est-à-dire de la couleur. Cela s'observe pour les matériaux comme le verre : les rayons bleus sont plus déviés que les rayons rouges et les couleurs sont ainsi séparées. Cette observation est connue dans le cas des prismes.

La variation de l'indice de réfraction d'un milieu transparent dans la lumière visible suit une loi dite de Cauchy : . où λ₀ est la longueur d'onde dans le vide et où A (sans unité) et B (en mètre carré) caractérisent le milieu. On remarque que pour un milieu non dispersif, B = 0 et qu'un milieu est de moins en moins dispersif si B tend vers 0.

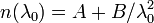
Conséquences

Une onde lumineuse est caractérisée par son spectre, qui est la répartition de l'intensité émise en fonction de la longueur d'onde. Dans le cas de la lumière visible, la longueur d'onde est reliée à la couleur perçue par l'œil. En général, une onde lumineuse est polychromatique, c’est-à-dire qu'elle est composée de plusieurs longueurs d'onde. Ainsi, la lumière du soleil contient la plupart des couleurs visibles. La dispersion va permettre de les séparer et de visualiser ainsi les couleurs qui composent le rayonnement, ce qui permet notamment de faire de la spectroscopie.

L'un des exemples visibles dans la vie courante est l'arc-en-ciel. L'arc-en-ciel observable à l'extérieur est le résultat de la dispersion de la lumière du soleil par les gouttelettes d'eau en suspension dans l'air. Le calcul du phénomène d'arc-en-ciel démontre que, pour le voir, il faut toujours tourner le dos au soleil ; c'est une chose facile à vérifier.

Mais la dispersion a aussi pour conséquence de limiter les performances des systèmes optiques. On peut citer :

• La dispersion chromatique dans les fibres optiques limitant la bande passante d'une transmission. Dans un milieu dispersif, chaque longueur d'onde se propage à une vitesse différente, d'où un élargissement temporel d'une impulsion lors de sa transmission. C'est pour cette raison, entre autres, qu'on utilise des diodes laser dont la largeur spectrale est faible.
• Dans les systèmes optiques, la différence de déviation pour chaque longueur d'onde implique un trajet différent selon la couleur, ce qui entraîne les aberrations chromatiques. Elles se manifestent par un point de convergence variant selon la longueur d'onde, provoquant ainsi une colorisation erronée de l'image. Voir à ce sujet les articles lunette astronomique et Microscope optique, par exemple.

Caractérisation des milieux dispersifs

Pour mesurer un indice de réfraction dans un milieu dispersif, il faut une radiation monochromatique de référence, comme la raie D de l'hélium (longueur d'onde dans le vide 587,6 nm), proche du milieu du spectre visible, qui est souvent utilisée.

Pour la radiation D, l'indice absolu n_D de l'eau à 20°C est de 1,333 ; celui d'un verre ordinaire est compris entre 1,511 à 1,535. L'indice de l'air est égal à 1,000 292 6 dans les conditions normales de température et de pression, mais il dépend aussi de la longueur d'onde dans le vide. Une différence (n − 1) aussi faible est mesurée, avec cette précision, par interférence entre deux rayons lumineux dont l'un passe dans l'air tandis que l'autre passe dans un tube vidé d'air. C'est la légère différence d'indice entre le vert et le rouge qui produit le “rayon vert” au coucher du soleil sur la mer (par très beau temps sans nuage) : la lumière verte est un peu plus déviée que la lumière rouge par la traversée très oblique de la couche d'air ; et de ce fait, le dernier rayon vert disparait une ou deux secondes après le dernier rayon rouge.

Dans le domaine du visible (longueurs d'onde dans de vide comprises entre 380 nm et 780 nm) la dispersion est caractérisée par la constringence. On classe alors les verres en type Crown (moins dispersif) ou Flint (plus dispersif) suivant que la constringence est inférieure ou supérieure à 50. La constringence, encore appelée nombre d'Abbe, est définie par la formule :

,

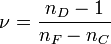
F et C désignant deux raies de l'hydrogène (longueurs d'onde dans le vide λ_F = 486,1 nm et λ_C = 656,3 nm)

Dispersion par un prisme

La dispersion par des matériaux tels que le verre a été utilisée pour analyser la lumière du Soleil. Les expériences de Newton à l'aide de prismes sont célèbres. Dans les expériences de démonstration, on utilise toujours des prismes qui, lorsque la lumière franchit les deux dioptres, permettent d'observer une bonne dispersion des couleurs.

Dans la pratique, on utilise aussi des « prismes à vision directe » qui sont en réalité des systèmes optiques constitués de 3 prismes accolés, choisis de façon à minimiser la déviation tout en optimisant la dispersion.

Dispersion par un réseau

Un réseau est une plaque transparente, rayée (plusieurs centaines de rayures parallèles/mm) ce qui est équivalent a des fentes. On peut donc avoir des interférences.

Pour une simple radiation on obtient une alternance de franges. Pour une lumière blanche, ce sont des dégradés de couleur que l'on observe autour d'une frange centrale blanche, celle-ci formant un axe de symétrie.