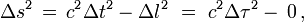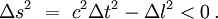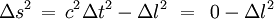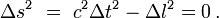Intervalle d'espace-temps - Définition
La liste des auteurs de cet article est disponible ici.
Relation entre événements
Le carré de l'intervalle spatio-temporel entre deux événements peut être de trois types différents :
- genre temps,
- genre espace,
- genre lumière.
Le genre d'un carré d'intervalle d'espace-temps dépend de son signe, et comme il est invariant par changement de référentiel inertiel, le genre d'un intervalle d'espace-temps sera le même pour tout observateur. Ainsi, on pourra remarquer que si deux événements sont séparés par un carré d'intervalle d'espace-temps de genre temps ou lumière, ils peuvent être liés par un lien causal direct, par contre s'ils sont séparés par un de genre espace, ils ne le peuvent pas, et ceci quel que soit l'observateur et son référentiel inertiel.
Genre temps
Si l'intervalle temporel cΔt l'emporte sur la distance spatiale Δl l'intervalle est dit du genre temps et l'intervalle d'espace-temps est positif :
Ce cas correspond à la situation où | Δl / Δt | < c , ce qui signifie que dans le référentiel où les mesures ont été faites, un mobile allant à la vitesse constante | Δl / Δt | dans la bonne direction peut être à l'endroit exact et au même instant que le premier évènement, puis, après son déplacement, à ceux du deuxième. Par conséquent dans le repère (inertiel) de ce mobile les deux événements se situent au même endroit, mais pas au même moment. Dans ce référentiel particulier, et d'après l'invariance du carré de l'intervalle d'espace-temps, l'écart de temps Δτ séparant les deux événements est appelé le temps propre les séparant, et est donné par la formule :
laquelle montre que le temps propre Δτ est donné par
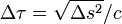
Dans ce cas d'un intervalle de genre temps, les deux événements peuvent être liés par un lien causal : par le biais d'une particule allant assez vite d'un événement vers l'autre, ou d'une influence véhiculée par de la lumière allant de l'un vers l'autre et dont l'effet déclencherait par la suite le deuxième événement, ...
Genre espace
Si l'intervalle spatial Δl l'emporte sur l'intervalle temporel cΔt, l'intervalle est dit du genre espace et le carré de l'intervalle d'espace-temps est négatif :
Ce cas correspond à la situation où | Δl / Δt | > c , ce qui signifie que dans le référentiel où les mesures ont été faites, aucun mobile allant à une vitesse inférieure à celle de la lumière ni aucun signal lumineux ne peut être à l'endroit exact et au même instant que le premier évènement, puis, après son déplacement ou sa propagation, à ceux du deuxième. Il ne peut donc pas y avoir de lien causal entre les deux évènements. On peut montrer qu'alors il existe un référentiel inertiel dans lequel les événements sont simultanés : dans ce référentiel, l'écart de temps entre les deux événements est nul, d'où
Ainsi, dans ce référentiel inertiel particulier, l'écart de temps est nul entre les évènements et leur distance spatiale, appelée distance propre, est
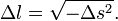
Genre lumière
Si le carré de l'intervalle spatio-temporel est nul, cela veut dire que la lumière parcourt exactement la distance géométrique entre les deux événements pendant le laps de temps séparant ces deux événements.
Ce cas correspond à la situation où | Δl / Δt | = c , ce qui signifie que dans le référentiel où les mesures ont été faites, seuls les particules de masse nulle, donc allant à la vitesse de la lumière, peuvent joindre les deux évènements. La vitesse de la lumière étant la même dans tous les référentiels inertiels, il en est de même quand ces événements sont vus depuis tout autre référentiel inertiel. Cela laisse encore la possibilité d'un lien causal entre les deux événements, un lien se faisant à la vitesse de la lumière.
Exemple : si l'événement A consiste en l'envoi d'un signal laser depuis la Terre vers la Lune et l'événement B consiste en la réception de ce signal sur la Lune, l'intervalle spatio-temporel entre A et B sera nul puisque la distance Δl entre Terre et Lune sera justement égale à la distance cΔt parcourue par la lumière pendant le temps Δt. Dans ce dernier cas on peut dire que l'intervalle est du genre lumière.